Lunar/Solar Tides and Pendulum Clocks (part 1)
Tom Van Baak, tvb@LeapSecond.com
The theory behind variations in the acceleration due to gravity is explained in some detail.
The value of g and the subtle lunar/solar tidal effects on g are calculated. This
tutorial is relevant
background to a discussion about the performance and limitations of precision pendulum clocks, such as Shortt,
Fedchenko, and Hall's Littlemore.
Calculation of g
Before we jump into details of tides let's review some basic physics.
To first approximation, the pendulum period equation is T = 2π√(L/g),
where T is the period, L the length of the pendulum, and g is the acceleration
due to gravity. Here on the surface of the Earth g has an approximate value of 9.8 m/s² (or 32 ft/s², 980 cm/s², 385 in/s², 32
ft/s²). In the field of gravity research g is often measured in units of Gals,
where 1 Gal = 1 cm/s². Thus g is about 980 Gals, or 980,000 mgal (milligals),
or 980,000,000 µgal (microgals).
Where does the value of g come from? The force of gravity on an object is, to
first
approximation, F = GMm/R², where M is the mass of the Earth, m is the mass of
the object, and R is the Earth's radius. Converting force to acceleration (F =
ma) and canceling m's we arrive at a simple expression for the acceleration due to
gravity: F/m = g = GM/R².
The universal gravitational constant, G (so-called big G), is 6.6742×10-11
m³/s²/kg. The mass of the Earth, M, is 5.9736×1024 kg and the
radius of the Earth, R, is approximately 6372 km. Doing the math, the acceleration due to
gravity, g (so-called little g), is about 9.82 m/s².
In short, the value of g that we have memorized is not a magic mathematical
constant, it is simply a function of Earth mass, density, and distance.
Variations in g, Space
Since Earth has
a slight equatorial bulge g clearly varies by latitude. Note that g varies by the square of the
radius so this effect is amplified. In addition
the value of g is affected by such local factors as proximity to large mountain masses, subsurface density
variations (due to mineral ore, oil, gas, or seasonal water table),
and elevation above mean sea level.
Although the nominal value for the acceleration due to gravity at the Earth's surface
is 9.8 m/s², g ranges from 9.76 to 9.83 m/s² depending on location. That's
more than a 0.5% variation! As one example, my theoretical calculations predict g here in Seattle (latitude ~47.6°) is
9.8085 m/s² while g in San Francisco (latitude ~37.8°) is 9.7997 m/s².
The net difference of 0.0088 out of 9.8 is about 900 ppm (90 ppm / degree of latitude).
Wow!
Similarly while g here at sea level is 9.8085 m/s², g at the summit of nearby Mt
Rainier (14411 ft, 4392 m) is 9.8133 m/s²; a difference of 0.0048 out of 9.8, or about 500
ppm (11 ppm per 100 meters of elevation). In horological terms (one second a day is about 11 ppm), these two examples represent
a clock rate error of about 77 and 43 seconds a day.
We can appreciate why, in previous centuries, a pendulum clock was the scientific instrument
best suited to measure
the shape of the Earth. We take for granted that pocket watches keep the
same rate anywhere in the world. But one man's error is another man's signal:
modern laser-based,
free-fall gravimeters have a sensitivity of
about 1 µgal and are used in mineral and oil exploration.
In short, the value of g that we have memorized is not even a constant; it is a function
of where on the planet you are. The local and global spatial variations are on the order of
hundreds or thousands of ppm.
Variations in g, Time
If a precision pendulum clock were attached to a solid wall or
stone foundation at a fixed location on Earth would g then be constant? No, although location is a large
factor, it is not the only factor. Being massive and nearby (in an astronomical
sense), the Sun and Moon have a non-zero effect
on the gravitational force on an object.
Picture what
happens when the Moon is directly overhead. While the Earth is strongly pulling the pendulum down with
an acceleration of
1 g, the Moon is weakly pulling the pendulum up towards itself. The result is
that g will decrease slightly. Similarly, when the Moon is on the opposite side of the Earth the pendulum is pulled down by
the combined forces of both the Earth
and the Moon. The result is that g will increase slightly.
The above is a simple but not technically correct explanation for variations
in g over time. To be more precise realize that tides are the result of a differential
force.
The way to think of it is not that the Moon is pulling one direction and the
Earth the other. The proper interpretation is that the acceleration caused by
the Moon is stronger for near objects than for far objects (and not just
inverse, but inverse squared). When the Moon is
overhead, from the Moon's
perspective, the center of mass of the Earth is farther away than the center of
mass of the pendulum (which rests on the surface of the Earth).
The value of g that we have memorized is also not constant in time. It is
affected by the dynamic relationship between the Earth, Sun, and Moon.
Calculation of Tides, Moon
It's not hard to compute the differential acceleration. Let R be the radius of the Earth and D be the distance between the center of
the Earth and the center of the Moon. When the Moon is directly overhead, a
pendulum on the surface of the Earth is D-R away from the center of the Moon.
When the Moon is directly opposite the pendulum is D+R away from the center of
the Moon. The center of Earth remains D away from the center of the Moon.
Let Me, Mm,
and Mp be the mass of the Earth, Moon, and pendulum, respectively. The pendulum of mass Mp is accelerated towards the
Earth:
g0 = F/Mp = GMe/R²
The pendulum is also being accelerated towards the Moon:
F/Mp = GMm/(D-R)² when the Moon is directly overhead,
or
F/Mp = GMm/(D+R)² when the Moon is directly below
The Earth is being accelerated towards the Moon:
F/Me = GMm/D²
The differential (tidal) acceleration on a pendulum on the surface of the
Earth due to the Moon is then:
GMm/(D-R)² -
GMm/D², which expands to
GMm ( D² - ( D² -
2DR + R²) ) / ( D² (D-R)² ), which simplifies
to
GMm ( 2DR - R² ) / ( D² (D-R)² )
Now since R << D (R = 6.372×103 km, D = 3.844×105
km; R/D = 0.016) we arrive at this close (within 1%) approximation to the differential
acceleration:
GMm2R/D³
With this formula we can now calculate the magnitude of the tidal effect of the Moon.
Using Mm = 7.347×1022 kg and Dm = 3.844×105 km,
the size of lunar tides is gm = 1.10×10-6 m/s². In units of
g, this is 1.12×10-7 g, or about 0.11 ppm of g.
Calculation of Tides, Sun
Using the same formula we can also calculate the magnitude of the tidal
effect of the
Sun. The Sun is so much more massive than the Moon (about 27 million times!) one
might expect it to have the dominate effect. But it is also much further away (about
390 times) and since tidal effects vary as the cube of the distance the net
result is that solar tides affect a pendulum only 45% as much as lunar tides
(never underestimate the power of inverse square or cube in
astronomy).
With Ms = 1.989×1030 kg and Ds = 1.496×108
km, the size of solar tides is gs = 5.05×10-7 m/s². Again in
units of g, this is 5.14×10-8 g, or about 0.05 ppm of g.
The tidal effects are additive. In the case where both the Sun and Moon are
aligned overhead the tidal effect on g is gm + gs, or 1.63×10-7 g.
When not overhead the tidal forces are correspondingly less based on the
geometry. In general, the value of g experienced at any instant by a pendulum can be represented
as:
g = g0 + gm(t) + gs(t)
where g0 is the fixed acceleration of gravity at some location due
to the Earth
alone (ignoring the rest of the universe)
and gm(t) and gs(t) are the time-varying tidal
acceleration effects of the Moon and Sun, respectively. With an inverse cube
effect you can guess that none of the other
planets in the solar system have a relevant contribution to tides.
Accurate calculation of gm(t) and gs(t) for any
time is complicated
by many factors. If the Sun or Moon is not directly overhead the effect varies
according to the trigonometry of the angles.
The Earth is tilted 23 1/2°.
The distance from the Earth to the Sun varies since the orbit of the Earth
around the Sun is elliptical, not circular. Same for the Moon. The distance to the Moon varies
from 363,104 km to 405,696 km. The plane of the orbit of the Moon is inclined 5.1°
with respect to the Earth-Sun plane. The Earth itself spins while all this is going
on.
 There is precession of the orbits; of the plane of the orbits; of the axis
of rotation(s). There's nutation; polar motion. The surface mass of the Earth is deformed due to tides, further affecting the
calculations. A so-called Love number correction can be applied based on the
density and fluidity of the mass. There's more than I understand, to be sure.
There is precession of the orbits; of the plane of the orbits; of the axis
of rotation(s). There's nutation; polar motion. The surface mass of the Earth is deformed due to tides, further affecting the
calculations. A so-called Love number correction can be applied based on the
density and fluidity of the mass. There's more than I understand, to be sure.
But astronomers love this sort of complexity and with no small number of lines of computer code it is possible to calculate
the actual position of the Sun and Moon in the sky and compute the net lunar/solar correction to g for any place and time on Earth.
Ocean tides are even more complicated since they depend on time-delayed sloshing
liquids, on topography of bays and ocean shores; levels of differential
acceleration not relevant to the simple case of the point mass of a
pendulum.
It is as if dozens of celestial gears are in motion, all of them
turning at different rates, none of them in phase, each of them affecting
gravity slightly, and the effect on a pendulum clock is the temporary sum of all gears
at any given instant. The analogy is appropriate: above, for example, is a photograph of
an old mechanical tide predicting machine, made from cables, pulleys, shafts,
dials, and yes ... gears.
So the value of g that we have memorized is neither constant in space nor in time.
Due to the effects of the Moon and Sun g is a complex function of time; the
temporal variations
are on the order of a tenth ppm.
A Graphical View of Tides
The following plots show calculated changes in g over time for Seattle. The
scale for each plot is the same: ±200 µgal, with positive values representing upward pull. Since g = 980,000,000 microgals, 1 µgal is about 10-9 g (a
nano g).
Typical tidal variations of g here are approximately +150 µgal to -100 µgal,
which seems to agree well with theory presented above (note 200 µgal is about
0.2 ppm g).
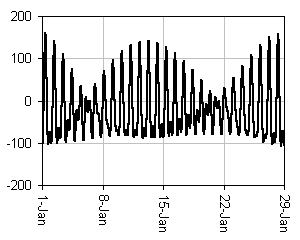
The first plot below is one-week in duration; the second plot is one-month in
duration.
Note large daily and weekly wiggles. In these plots roughly 12 & 24 hour cycles
(Earth rotation related) are clearly visible, as well as roughly 14 & 28 day cycles (Moon
orbit related).
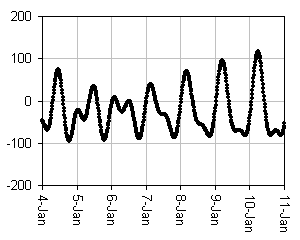
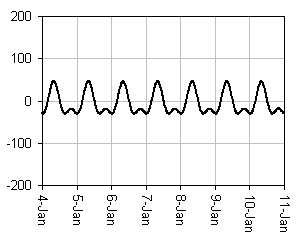
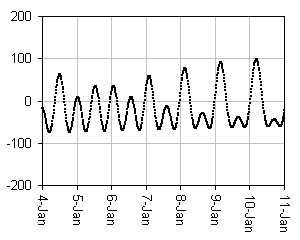
The plots clearly reveal multiple cycles superimposed. To better understand
this, the first plot below is the solar-only component of the 1-week plot above;
the second plot below is the lunar-only component.
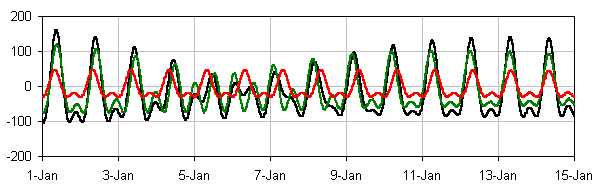
Below is a 14-day composite color plot of the above (sun, red; moon, green;
total,
black):
Tidal acceleration plots for different locations on Earth and different time spans reveal other patterns.
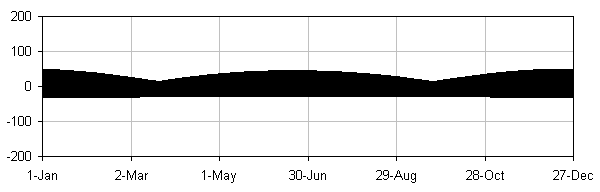
Below are three plots for the full year, 2006, for Seattle.
Solar tides only (note annual cycle and equinox points):
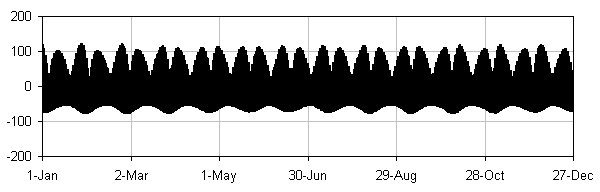
Lunar tides only (note strong 14 & 28 day cycles and slight asymmetry):
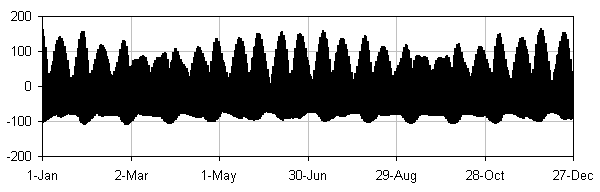
Combined tidal effect (gravitational sum of lunar and solar
effects):
Note also that due to the complex, non-synchronous nature of the cycles the sum of
successive positive and negative variations of g do not necessarily cancel out over
a day, a week, a month, or even a year.
Clearly a long-term average is better than a short-term average but no amount of
averaging will lead to
a complete cancellation.
The rate of change of g is also of interest to a pendulum clock. A
change of 0.1 ppm gradually over a few weeks is different than the same change in g
over a few hours. From the graphs the rate appears to be as much as 200
µgal in as little as 4 hours, which translates to a certain rate of period change, equivalent
to a "rate of rate" of time (also called
frequency drift).
Math with Small Numbers
A short aside is useful here. When doing math with very small numbers it is often easier to put
away the calculator and use shortcuts instead. Consider T = 2pÖ(L/g).
It's clear that if L quadruples then T doubles; if g is quartered then T halves.
That's easy. But what happens to T if g goes up or down by only 0.1 ppm? First
note that saying "g goes up 0.1 ppm" means "g + 0.1 ppm of g"
which is g × (1 + 0.1 ppm), or g × 1.0000001.
If you consider that 1.1² = 1.21 or 1.01² = 1.0201 or 1.001² = 1.002001 a pattern is clear. 1 plus 10-n squared is nearly exactly 1 plus 2×10-n.
In general, if e is a small number, both of the following are true:
(1 + e)² = 1 + 2 e
Ö(1 + e) = 1 + 1/2
e
Similarly, the pattern in 1/1.1 = 0.909 or 1/1.01 = 0.990099 or 1/1.001 =
0.999000999 confirms another pair of shortcuts:
1 / (1 + e) = 1 - e
1 / (1 - e) = 1 + e
Conclusion
We now see that if g goes up by e, then T goes
down by 1/2 e. Also since we now know that g
varies by about ±1×10-7 (2×10-7 total), we can conclude
that T varies by about ±5×10-8 (1×10-7
total). More on this later.
Putting this in horological perspective, note that a rate deviation of 1×10-7
is equivalent to about 3 seconds a year or about 8 ms per day, suggesting that a
pendulum clock has to
be stable to at least a couple of milliseconds a day before it can "detect
tides". If a pendulum clock is inherently stable to milliseconds a day then
tides will significantly limit and measurably affect its short-term performance. On the
other hand, if a pendulum clock is much less accurate than milliseconds a day then the
noise of lunar/solar tides will transparently join other noises in the clock;
the tides will be "lost in the noise".
In summary, the 9.8 m/s² value for g changes in the 2nd or 3rd decimal place
from location to location and changes in the 6th decimal
place from hour to hour. The temporal variations are bounded and predictable;
they average down over time, but never quite to zero. These "ripples" in g cause
variations in pendulum clock rate on the order of 1×10-7, which is
equivalent to milliseconds per day.
The perturbations of period become a source of gravity noise in any precision pendulum clock.
A more detailed analysis of that noise, the pendulum's response to a changing g,
and the ability of
the pendulum to detect the noise of tides is the subject of
the next section.
 There is precession of the orbits; of the plane of the orbits; of the axis
of rotation(s). There's nutation; polar motion. The surface mass of the Earth is deformed due to tides, further affecting the
calculations. A so-called Love number correction can be applied based on the
density and fluidity of the mass. There's more than I understand, to be sure.
There is precession of the orbits; of the plane of the orbits; of the axis
of rotation(s). There's nutation; polar motion. The surface mass of the Earth is deformed due to tides, further affecting the
calculations. A so-called Love number correction can be applied based on the
density and fluidity of the mass. There's more than I understand, to be sure.






