09-May-2005 data
01-Sep-2007 analysis
Below are plots from a long-term measurement of an Oscilloquartz 8607/008 BVA quartz oscillator. Let's play with Stable32 and see what the frequency drift rate is.
C:\tvb\tsc036\phm-8607> dir/os | tail LOG186~1 GZ 2,799,341 05-09-05 5:47a log18676.txt.gz C:\tvb\tsc036\phm-8607> gzip -d < log18676.txt.gz | wc 7.333 MB, 7509 KB, 7689048 chars, 548573 words, 548573 lines C:\tvb\tsc036\phm-8607> dir/od | more LOG18~12 GIF 23,900 05-06-05 11:00a log18689v.gif LOG18~13 GIF 21,739 05-06-05 11:02a log18690v.gif LOG18~14 GIF 14,245 05-06-05 11:03a log18691v.gif LOG18~15 GIF 35,136 05-06-05 11:04a log18692v.gif LOG186~1 GZ 2,799,341 05-09-05 5:47a log18676.txt.gz LOG18~16 GIF 23,980 05-10-05 1:02a log18698v.gif LOG18~17 GIF 22,299 05-10-05 1:03a log18699v.gif LOG187~1 GIF 14,228 05-10-05 1:03a log18700v.gif LOG187~2 GIF 35,978 05-10-05 1:04a log18701v.gif |
Below is a set of TSC 5110A snapshots taken near the end of the 6-day run.
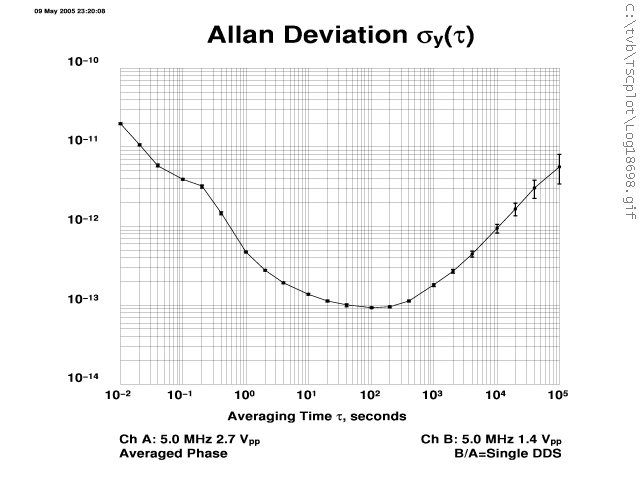
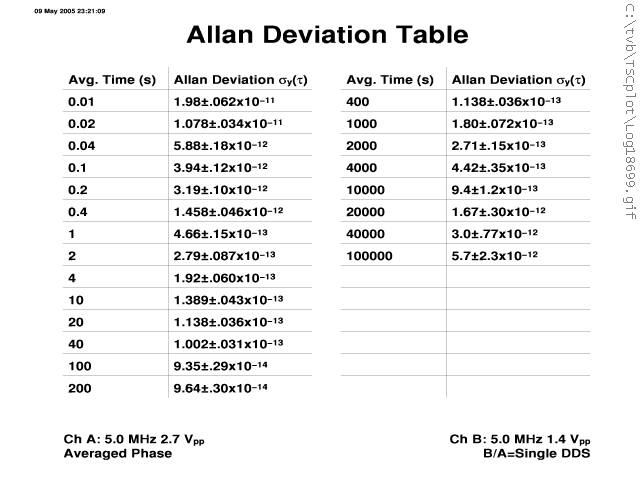
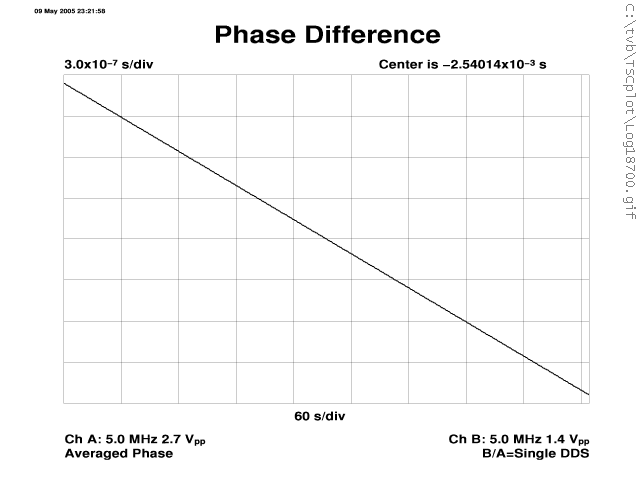
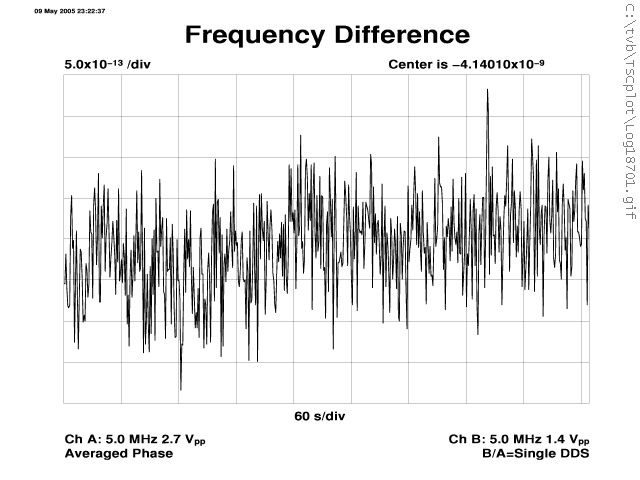
| OSA 8607 vs. PHM out to tau 100k |
 |
 |
 |
 |
Below a few more 10-minute duration frequency-deviation strip-chart plots for reference. With standard decade scales, these can be used for noise comparison with other frequency standards.
| Typical frequency plot re-scaled to 1×10-12/div, 1×10-11/div, and 1×10-10/div, respectively. |
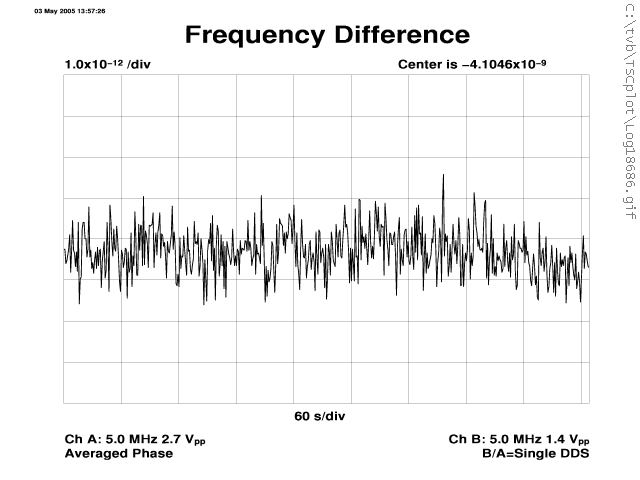 |
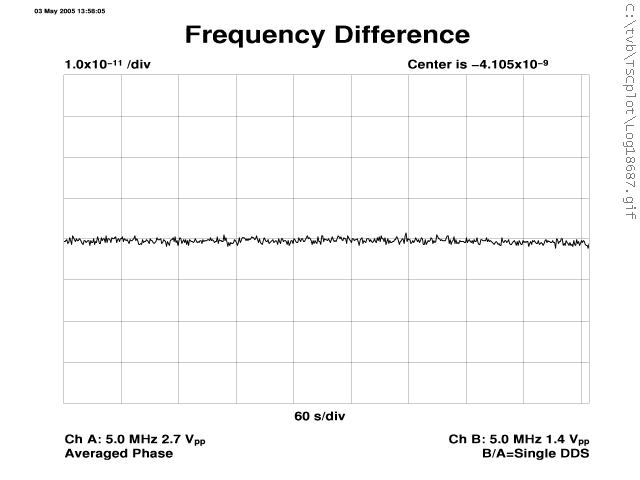 |
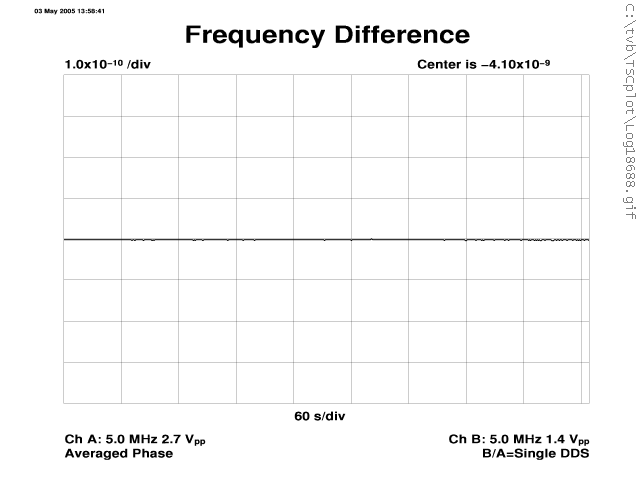 |
In addition to creating real-time ADEV plots and most-recent--ten-minute phase and frequency strip charts, the TSC 5110A outputs phase data at a 1 Hz rate. This data is logged to a PC and can then be analyzed off-line by tools such as Stable32. Phase differences are in units of period (200 ns in this case) which can be converted into seconds or ns as needed.
| Phase, raw
Notes: open log file as phase, with tau 1 s, with scale by 2e-7 (= 200 ns = 5 MHz); plot |
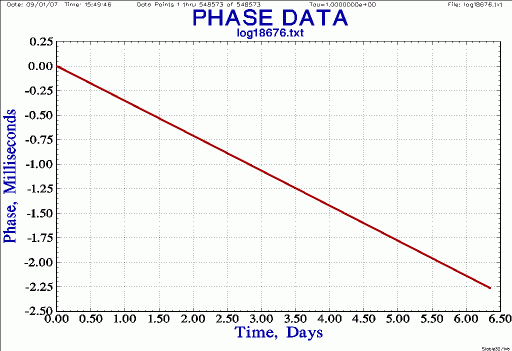 |
|
| Phase, frequency offset removed
Notes: phase slope is frequency offset; calculate and remove frequency offset (linear fit); re-plot |
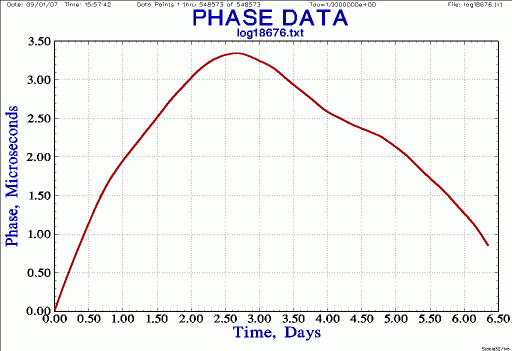 |
|
| Phase, frequency offset and drift removed
Notes: frequency slope is drift rate; calculate and remove frequency drift (quadratic fit); normalize residual phase; re-plot |
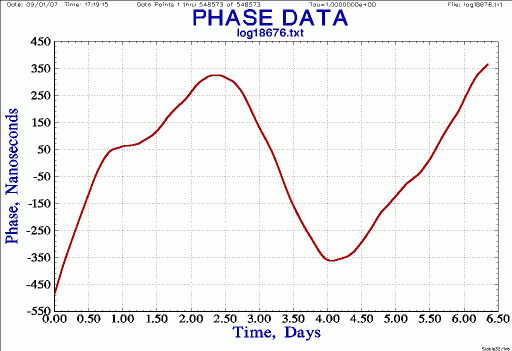 |
|
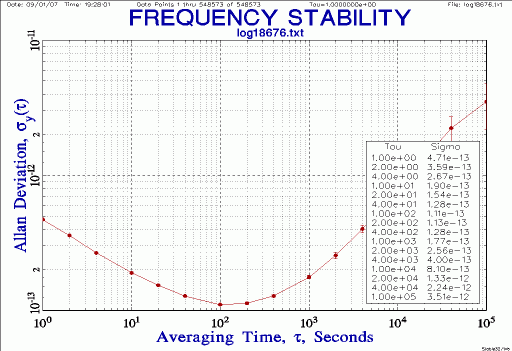
| Stability, Allan Deviation (tau 1 to 105
s)
Notes: run ADEV from raw phase data (no unfair drift removal at this point); 1-2-4-decade scale; plot |
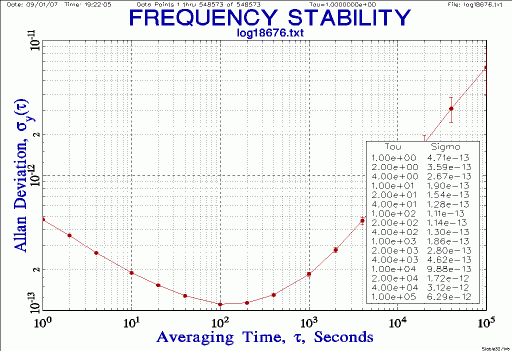 |
|
| Stability, Overlapping & Modified
Allan Deviation
Notes: run OADEV & MDEV from raw phase data; re-plot |
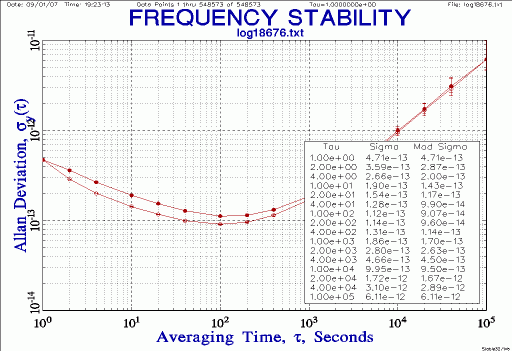 |
|
| Stability, Allan Deviation, drift removed
Notes: run ADEV from raw phase data, selecting remove drift; re-plot |
 |
|
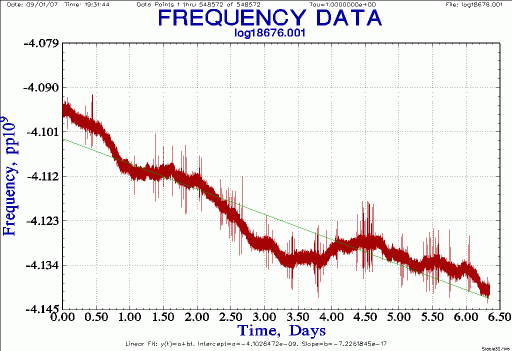
| Frequency, raw
Notes: conv raw phase to frequency; plot |
 |
|
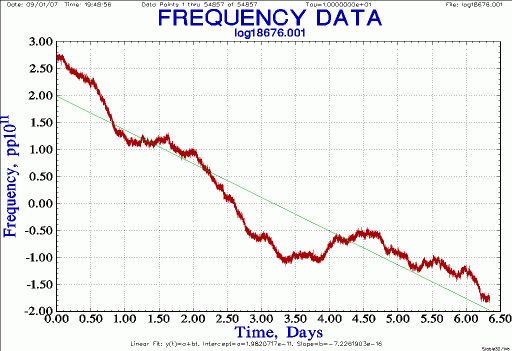
| Average frequency
Notes: average by 10x (10 s samples); normalize (remove mean frequency); add linear trend line (frequency drift) but do not remove drift; re-plot |
 |
|
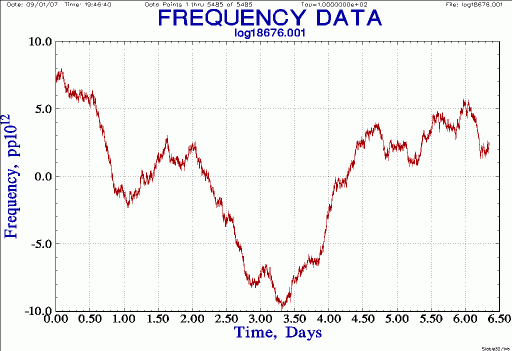
| Average frequency, drift removed
Notes: average again by 10x (now 100 s samples); remove frequency drift; normalize; center scale to ±10×10-12; re-plot |
 |
|
| Phase/Frequency jumps
Notes: open phase, conv phase to freq, use check and stats to look for spikes. Note sample numbers, go back to phase, use stats to zoom in; extract nice 10 minute record using part; [i5500 n600]; use 599 points (not 600); remove slopes and normalize both phase and frequency; plot each |
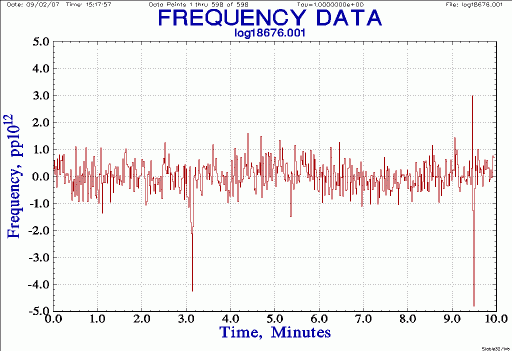
|
|