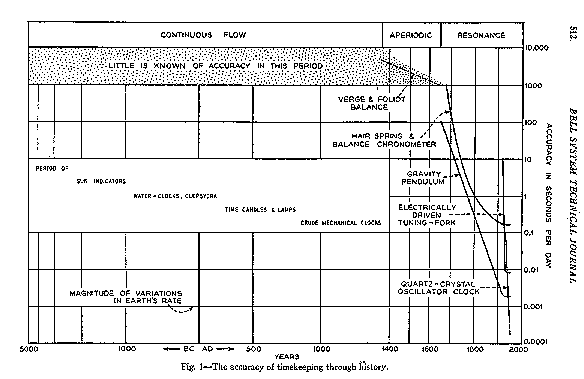
Fig. 1 - The accuracy of timekeeping through history.
Reprinted from The Bell System Technical Journal, Vol. XXVII, pp. 510-588, 1948. Copyright 1948, AT&T. All rights reserved. Reprinted with permission.
The Evolution of the Quartz Crystal Clock*
By WARREN A. MARRISON
THE EPOCH OF APERIODIC CONTROL
THE EVOLUTION OF ELECTRIC OSCILLATOR CLOCKS
SOME of the earliest documents in human history relate to man’s interest in timekeeping. This interest arose partly because of his curiosity about the visible world around him, and partly because the art of time measurement became an increasingly important part of living as the need for cooperation between the members of expanding groups increased. There are still in existence devices believed to have been made by the Egyptians six thousand years ago for the purpose of telling time from the stars, and there is good reason to believe that they were in quite general use by the better educated people of that period. 1 Since that period there has been a continuous use and improvement of timekeeping methods and devices, following sometimes quite independent lines, but developing through a long series of new ideas and refinements into the very precise means at our disposal today.
The art of timekeeping and time measurement is of very great value, both from its direct social use in permitting time tables and schedules to be made, and in its relation to other arts and the sciences in which the measurement of rate and duration assume ever increasing importance. The early history of timekeeping was concerned almost entirely with the first of these and for many centuries the chief purpose of timekeeping devices was to provide means for the approximate subdivision of the day, particularly of the daylight hours.
The most obvious events marking the passage of time were the rising and setting of the sun and its continuous apparent motion from east to west through the sky. The first practical measure of the position of the sun of which any record is known was the position or the length of shadows of fixed objects, resulting through a long period of development in the well-known sundial in its many forms. But the sundial was in no sense an instrument of precision and in no sense could be considered as a time keeping device. Even after the development which resulted in mounting the gnomon parallel with the axis of the earth, the largest, most elaborate, and most carefully made instruments could at best indicate local solar time. Furthermore, the sundial has value only in daylight hours and then only on days when the sun shines clearly enough to cast a shadow. These shortcomings became more and more important with advances in society and, for measuring duration, man soon began inventing timekeeping means that would work without benefit of the sun.
The evolution of timekeeping devices may be divided into three main periods, each employing a specific type of method, although overlapping to some degree in their applications, and characterized by increasing orders of accuracy.
A graphical representation of this evolution, indicating these three periods of development, and showing the relation between some of the major contributions to time keeping and the resulting accuracy of time measurement, is shown in Fig. 1. The methods employed chiefly during these three periods may be classified broadly as CONTINUOUS FLOW from the beginning up until about 1000 A.D., as APERIODIC CONTROL from then until about 1675 A.D. and as RESONANCE CONTROL from that time up to the present. Keeping in mind the logarithmic nature of the time and accuracy scales used in this graph, it can be seen readily that most of the advancement has been made in a very small part of the total time, corresponding to the resonance control epoch.
Fig. 1 - The
accuracy of timekeeping through history.
----------------------------
* The subject matter of this paper was given before the British Horological Institute in London on the occasion of the presentation of the Horological Institute's Gold Metal for 1947 to Mr. Marrison in consideration of his contribution toward the development of the quartz crystal clock. The present text is substantially as published in the Horological Journal.
----------------------------
Perhaps due to a feeling that the passage of time was like the flow of some medium, the first time measuring devices were those depending on the flow of water into or out of suitable basins.
It was recognized that, with an orifice properly chosen, the time required to fill or empty a given basin should be about the same on repetition, and hence was born the first reliable means for measuring time at night or on overcast days. A great variety of devices operating on this principle were constructed and used, some of the earliest having been made by the Babylonians and the Egyptians 3500 years ago.
Some of these water clocks, or clepsydra as they were called, had floats or other indicators which were intended to subdivide a unit of time into substantially uniform divisions. Others were constructed so that successive fillings of the basin would be counted or would operate a stepping device, associated with a dial or other indicator. Through the centuries great numbers of such devices were constructed, with some of the later ones having elaborate mechanisms for striking the hours or for animating figures of people or animals.
For use in places where water was not readily available and where sand was plentiful, clepsydra were developed that would operate with the flow of sand in much the same way as with the flow of water. The basic ideas were not greatly different, the substitution being merely one of expedience.
The hour glass, and its smaller counterparts, is one of the most convenient forms of this device and until quite recent times served a useful purpose where accuracy was of no great importance. The hour glass shown in Fig. 2 was used by a pastor in the early eighteen hundreds to determine the length of his sermons. The average variation among a set of ten one-hour determinations made recently with this glass was 3 minutes, or about 5 per cent.
The clepsydra that were designed to repeat and totalize an endless succession of cycles were especially adaptable to the measurement of extended intervals of time, although with very poor accuracy as we now think of it.
Fig. 2 - Hour
glass.
By suitable design any desired number of cycles could be made equal to the natural large unit, the day, so that any fraction of a day within the accuracy of a given instrument could be determined simply by counting off the number of cycles from a particular starting point such as sunrise, sunset, or high noon. It was possible with these devices to operate without calibration over periods of several days, although the cumulative error inevitably was very large.
An error of a few hours was of small importance in the days when the speed of communication and travel alike depended on pack animals or the caprices of the wind. And so, in spite of the inaccuracies of the water clocks and sand clocks, they served their purpose well through many centuries. In fact, it was not until the tenth century A.D. that any really novel effort was made to improve upon them as timekeepers. The first efforts to improve upon them, making use of falling weights for motive power and various frictional devices to control the rate of fall, were not very successful because no satisfactory means were known to keep a friction-controlled device sufficiently constant for the job. Clocks so constructed were no better timekeepers on the whole than the traditional clepsydra. They had, however, the hope of compactness, and much ingenuity was exercised in their design over several centuries.
Also in the category of continuous flow devices should be mentioned the methods depending on the rate of burning, such as in time candles, time lamps and their numerous variations. Such timekeepers are not very accurate but are thoroughly reliable in dry, quiet places, even providing their own illumination at night. Such timekeepers are known to have been used before the tenth century A.D. and certain variations still are used by a few isolated tribes, especially in the tropics.
THE EPOCH OF APERIODIC CONTROL
In or about the year 1360 the invention of an escapement mechanism for controlling an alternating motion from a steady motive power, such as a suspended weight, was the first really important step in the history of precision clock development, and marks the beginning of the second major epoch in timekeeping evolution. The escapement in one form or another was soon applied in practically all timekeepers, the most outstanding example of an early application being a clock constructed by Henry De Vick for Charles V of France in or about the year 1360 A.D. and still in use—with extensive modifications—in the Palais de Justice in Paris.
This invention was important, not because De Vick's clock, or any of its immediate successors, were good timekeepers, but because this was the first time that vibratory motion in a mechanism was used deliberately to control the rate of a time-measuring device. All precision clocks depend in one way or another on using energy to produce vibratory motion, and on using the rate of that motion to regulate suitable dials and other mechanisms.
No simple improvement on De Vick's clock could ever have produced a precision clock in the modern sense, however, because the essential rate-controlling feature was still lacking. His invention consisted of the use of a verge escapement which produced oscillatory motion in a dynamically balanced member, known as a foliot balance, having essentially only moment of inertia and friction. The rate of oscillation, therefore, depended to a large extent on the applied force exerted by the falling weight through a train of wheels, and upon the friction of the escapement parts and of the oscillating member itself.
This sort of operation is known sometimes as relaxation oscillation and appears in many forms. In the clock, the rate-controlling feature depends upon the length of time it takes a member having a given moment of inertia to move from one angular position to another under a given applied torque. Thus, the rate depends to first order on the applied torque.
Although De Vick's clock was one of the most famous in all history, it was not because of its good record of timekeeping. In its original form, it is said that it often varied as much as two hours a day from true time. Outwardly, this clock on the Palais de Justice appears about the same as it did originally, but the "works" have been modernized and it keeps much better time now.
The history of timekeeping during the next three hundred years consisted mainly in improvements and in a great variety of applications of the principles contained in De Vick's clock. During this period great numbers of clocks of all sizes, from tower clocks to portable table clocks were made, controlled by various forms of the crown wheel, verge and foliot balance. All of these timekeepers belong to the class that we have just called aperiodic. Their accuracy, in general, was still poor and the indicator on their dials consisted of but one hand—the hour hand. It was not until the invention and application of the pendulum that the next major improvement was born in timekeeping.
All that has been said so far is a prelude to the shortest but by far the most productive epoch in timekeeping, that of resonant control. The heart of every precision clock is an oscillatory device which depends upon resonance for its constancy of rate. The history of precision clock development consists largely of the choice and design of stable resonant elements and of devising means for using them so that as far as possible their inherent properties alone control their rates of oscillation. Once in stable oscillation, it is only necessary to control the indicating of dials and other suitable mechanisms in order to constitute a complete clock.* Presumably this can always be done, but in some cases it is more convenient to do than in others, as will appear.
The resonant element may be any of a wide variety of forms, mechanical or electrical, all characterized by the single property that, if deformed from a rest condition and released, the stored energy is transformed back and forth from potential to kinetic at a rate depending chiefly on the effective mass and the effective stiffness, or other like properties, a small proportion of the energy being lost in internal friction at each oscillation. Some resonant elements which have been used in timekeepers are illustrated in Fig. 3.
Fig. 3 -
Typical resonant elements used in timekeeping.
The simplest appearing of all these is that of a mass, M, supported by a spring with stiffness, S. From the equation of motion
the period of oscillation may be derived simply and is found to be
Similarly for the simple electrical resonant circuit where current flowing in an inductance, L, behaves like a mass, and current flowing in a condenser, C, behaves like the reciprocal of a stiffness, the period may be written.
* Encycl. Brit. 14th Ed. "A clock consists of a train of wheels, actuated by a spring or weight or other means, and provided with an oscillating governing device which so regulates the speed as to render it uniform." Similar expressions are derivable for the periods of oscillation of all simple oscillating systems, including the pendulum for which the period (for small amplitudes) is given by
where 
and 
are respectively the length and gravity expressed in the
same system of units, for example, the c.g.s. system.
When any such resonant element is strained from its rest condition, and released, it will oscillate with gradually decreasing amplitude until all of the stored energy has been dissipated in internal friction or resistance, and in the friction or resistance of the coupling with the supports. In general, the resulting amplitude of free oscillation may be given as
the
graph of which is a damped sine wave. The rate of free oscillation,
, is
dependent chiefly on the effective mass and stiffness and to a small
degree on the effective resistance of the element, while the rate of
loss of amplitude, that is, the logarithmic decrement, 
, is dependent
on the ratio of effective resistance to effective mass.
If the resistance could be made exactly zero, such a motion once started would continue forever and its rate would be controlled wholly by the effective mass and stiffness of the resonant element. Actually, of course, such a condition cannot be realized in practice but, by the selection of suitable materials and environment, and by special control means, it is possible to approach very closely to the ideal condition by causing the oscillation to be maintained almost as though there were no damping.
The evolution of precision timekeeping, whether consciously or not, has centered around the study and development of these two ideas: to discover resonant elements whose rate-determining properties are inherently stable, and to discover means for sustaining them in oscillation as though they had no effective resistance; or in employing means to circumvent or to compensate for any such resistance. The high precision of rate control that can now be obtained has been the result largely of developments in these two categories.
The Pendulum
The gravity pendulum was the first truly resonant element to be used to regulate the rate of a clock and for nearly three centuries maintained the supremacy for precision measurements of time. The pendulum was more a discovery than an invention, the popular story of its origin being that, while still a youth of seventeen years, Gallileo Galilei chanced to notice that a hanging lamp in the Cathedral of Pisa seemed to swing at the same rate regardless of amplitude. This he confirmed approximately by comparison with his pulse, and later made an extensive study of the isochronism of swinging bodies. These studies were in progress as early as 1583. Nearly sixty years later Gallileo described to his son Vincenzio how a pendulum could be used to control a clock, but no concrete result of this advice is known to have been made at that time. A working model of this clock, made subsequently from the original drawings, is on exhibition in the South Kensington Science Museum, London. The first authentic record of the actual use of a pendulum in a clock is attributed to the great Dutch scientist, Christian Huygens, who produced his first pendulum clock in 1657. This was described by him in the Horologium in 1658.2
The performance of pendulum clocks was so good that almost immediately clocks of all other types were modified to include a pendulum. So complete was this transformation that very few unmodified clocks are now in existence which antedate the first application of the pendulum to timekeeping. This, as a matter of fact, is one of the major reasons that so little is known about the actual mechanisms used in mechanical clocks that were made before the introduction of the pendulum.
The subsequent history of pendulum clock development is well described in numerous books and papers and covers a wide field. Only those factors that relate the pendulum to other means of rate control will be discussed in the following.
The properties of a pendulum which make it such a good timekeeper are easily seen from a study of the forces on the bob as illustrated in Fig. 3. Since these forces must be in equilibrium at all times we may write (assuming no friction)
The nearly isochronous property of the pendulum is contained in this relationship since the period, on solution, is
where q is the maximum semi-amplitude of swing expressed
in radians. When this arc is small the period approaches a minimum.
For small angles the natural period depends almost wholly on the
ratio of 
to
and the
stability of 
depends chiefly upon the constancy of and . Figure 4 shows the
relation between period and the arc of swing, expressed as seconds
per day departure from the theoretical rate for zero arc.
Fig. 4 -
Relation between arc and rate of pendulum.
The sum of all the terms that depend upon
powers of sin 
/2 is known as the circular error, relating to the fact
that the bob is constrained to move on the arc of a circle. It was
shown theoretically by Christian Huygens3 that if the bob could be constrained to move on
the arc of an epicycloid it would be truly isochronous, that is, the
period would be completely independent of its amplitude of motion.
It is of interest to note at this point that in no other resonator
used for precision timekeeping is there the direct counterpart of
circular error, for in all other cases the restoring force varies
linearly with displacement in the region of operation and not as a
sine function of it.
In the early stages of pendulum clock development it was not necessary to consider the arc error because other errors were of greater magnitude. But it is by no means a negligible factor, and in all precision timing by pendulums it must be accounted for, either by allowing for an arc correction, as is done commonly in geodetic survey work, or by keeping the arc small and precisely controlling it. According to F. Hope-Jones4, referring to the master pendulum in the famous Synchronome free-pendulum clock: "A variation of only 0.01 mm. in the excursion of the bob or 2 secs. of arc will by circular error alter the rate by 0.00145 sec. per day, - and if it arose unperceived and was steadily maintained, it would produce an accumulated error of half a second in a year, so the necessity for this close observation is obvious."
The control of arc has almost invariably been accomplished by keeping constant the amount of energy applied per swing so that the actual amplitude obtained is that value for which all of the applied energy is dissipated in the pendulum system. In a sense this method of control of arc puts a penalty on improvements in design that would reduce the friction, because the better a pendulum becomes in this respect the less stable becomes the arc control. Since even the best pendulums develop unexplainable small changes in arc, it has been common practice in some observatories to record the arc frequently and to make allowance for changes in it when making the most precise time determinations.
The inherent constancy of rate of a
pendulum, with small or constant amplitude of swing, depends to the
one-half power on the stability of /. The changes in and are quite
independent of each other and so can be treated separately. Other
factors that will be described also affect the rate, and it is the
object in every precision clock design to reduce such variable
effects to the absolute minimum.
Some control can be exercised over every
factor except , which remains a property of space and is dependent only
on the proximity of matter and on acceleration. As is well known,
the value of varies over the surface of the earth due chiefly to its
deviation from spherical shape, and because of the uneven
distribution of matter. It also varies with vertical displacement or
tides at any location to such an extent that a gravity clock that
keeps accurate time at ground level will lose a second a day or more
in a tall building. Actually, it is now possible to chart variations
in with
high precision through measurement of the rate of a pendulum clock
against a standard whose rate does not depend upon
gravity.
Most of the factors that can affect have been
studied critically and means have been found to reduce them to very
small effects. The chief source of variation was at first the
temperature coefficient of the pendulum rod. With ordinary metals
the rod expands from 10 to 16 parts in a million per degree C,
causing a proportionate change in rate of half this amount,
corresponding to from one-half to two-thirds of a second per day.
Many ingenious means were developed to reduce this effect, starting
with George Graham's mercury-filled bob in 1721, followed by John
Harrison's grid-iron pendulum in 1726, and a great number of
variations on these ideas, all depending on the differential
coefficient of expansion of dissimilar materials.
About the year 1895, Charles Edouard Guillaume of Paris developed an alloy, consisting chiefly of nickel and iron, which he called Invar, because it had a very small temperature coefficient of expansion, from which pendulum rods could be made. The use of this material made it unnecessary to resort to complex compensated pendulums with their own inherent instabilities, and the accuracy of timekeeping was increased another step. The residual temperature effects could be measured readily, and compensated if desired, by the use of a small bar of aluminum attached to the bob.
Some other important factors that affect the working length of a pendulum are the aging of the supporting rod, the "knife edge" or spring used for the suspension, the nature of the main supporting column or frame, and some atmospheric effects caused by changing temperature and pressure. In the most accurate pendulum clocks, the atmospheric effects are greatly reduced by mounting the pendulum in partially evacuated, hermetically sealed enclosures which can be temperature controlled. All of these factors and many others are discussed in every good treatise on accurate pendulum clocks. They are mentioned here chiefly for the purpose of comparison with like factors in the quartz crystal clock and to show how in many cases the difficulties introduced by such factors may be more easily and more positively controlled.
In every primary clock mechanism the resonant governing device must be sustained in oscillation, and the manner in which this is done has a strong bearing on its rate regardless of the quality of the governing element. The basic requirements are the same for any kind of oscillator, whether a pendulum, an electrically resonant circuit comprising inductance and capacitance, a steel tuning fork, or a quartz crystal resonator. The requirements were first stated for the case of the pendulum by Sir George Airy in 1827 and it has always been the aim in the design of every good pendulum driving means to satisfy Airy's condition.
This condition is conveniently illustrated by the diagram of Fig. 5 which shows the two most familiar representations of damped sinusoidal motion. In order to provide a convenient scale in the drawing an impractically large damping is represented, corresponding to a Q of 20. The Q of a resonant circuit is related to the logarithmic decrement, d , by the relation Qd = p . The factor d is the logarithm, to base e = 2.718..., of the ratio of the amplitudes at any two successive periods. It should be noted that the Q of a good electrically resonant circuit is in the order of 200, that of a good pendulum from 10,000 to 100,000 and that of a good quartz resonator from 100,000 to 5,000,000. The significance of these higher values of Q will be evident from the following discussion.
Fig.
5—Amplitude-phase diagram for resonant element.
In Fig. 5 the damped sine wave shown corresponds, point by point, to the phase diagram, which is simply a logarithmic spiral. By suitable choice of scale the spiral can be interpreted to represent either the amplitude or the velocity—in which case the real amplitude is vertical and the real velocity horizontal. In this representation the velocity is shown maximum when the amplitude is zero, which is a very close approximation to fact for all practicable values of Q. The discussion will center on the velocity spiral.
Let us assume that the pendulum is
sustained in oscillation by a succession of short impulses, one for
each swing applied at some phase angle j 1. If the impulse
is really short, the velocity will be increased to the
value that the pendulum had when it occupied the same position
during the last swing. This change of condition is represented
by the short horizontal path on the velocity-phase diagram and, as
indicated, is accompanied by an advance in phase D j 1.
This can be interpreted as meaning that the period of a pendulum
sustained in oscillation in this way is reduced from its natural
period in the ratio of 
It is obvious from the
diagram that 
becomes smaller and that this ratio approaches unity as
the phase of the applied impulse approaches that of the maximum
velocity—that is, when the pendulum is in the center of its swing;
and this is Airy's condition. It is clear also that if the impulse
is applied after (instead of before) the instant of maximum
velocity, the period will be correspondingly increased. From the
geometry of the figure, it can be seen that, in the neighborhood of
the optimum condition, the deviation from natural period is very
closely proportional to the amount of the phase departure.
The closeness of spacing of the turns of
the spiral depends directly on the Q of the resonant element.
For a Q of 200, the turns will be packed ten times closer
than shown, and the corresponding 
will be only one tenth as
great, other conditions being comparable. For a Q of a
million or more, becomes very small indeed, especially when j is properly
chosen—and the variation in 
, which is a measure of
the variation in rate due to the driving means, may be made
vanishingly small.
The importance of the above properties to timekeeping depends upon how well conditions can be set up to realize them. At first wholly mechanical means were employed and, with the advent of the dead-beat and detached escapements and by careful design and operation, quite remarkable performance was obtained.
A new approach in timekeeping methods was introduced by Alexander Bain5 in 1840 when he first used electrical means for sustaining a pendulum in oscillation. The importance of Bain's invention of the electric clock is indicated by a long controversy over the priority of the invention with Charles Wheatstone, who was working along similar lines at the same time as a by-product of his extensive researches on the electrical telegraph. A brief story of this controversy entitled "The First Electric Clock" was written for the one-hundredth anniversary of Bain's invention6. The first electric pendulum clocks could not compare in accuracy with the best mechanically driven pendulums of the period but, in spite of a great deal of initial skepticism on the part of those brought up in the mechanical tradition, electrical maintenance and control has been applied in the most accurate pendulums in the world.
The free-pendulum clock makes use of the idea, first proposed by Rudd, of allowing a master pendulum to swing free of all sustaining or other mechanism for a considerable number of periods and of imparting to it, after each group of free swings, a single impulse large enough to maintain the next equal number. The advantage is that no friction effects of driving mechanism are coupled to the pendulum except during that minimum time required to impart energy to it. Actually, in theory, the phase error introduced by one large impulse after n free swings is exactly the same as the sum of the phase errors for n small impulses. That can be deduced from the phase diagram of Fig. 5. But experience has shown that a pendulum is actually more stable when the sustaining mechanism is detached from it the greater part of the time.
The Synchronome free-pendulum clock includes also the basic idea of the gravity remontoir first applied by Lord Grimthorp (then Sir Edmund Beckett Denison) in the design of the mechanism of Big Ben, London, constructed in 1854—and still in continuous operation. The ingenious application of these principles and the electrical means devised by F. Hope-Jones and W. H. Shortt for its accomplishment have resulted in the construction of the most accurate pendulum clocks in the world by the Synchronome Clock Company of London. The history and development of the free-pendulum clock is elegantly described by F. Hope-Jones in his book on Electric Clocks7.
The predominant characteristics of a pendulum resonator, as used in a clock, have just been discussed in order to show the parallel between them and the properties of other resonant systems. It will be shown how some of the factors that have been troublesome in the development of pendulums have been rather easily taken account of in other types of control devices and in particular in the quartz crystal clock.
THE EVOLUTION OF ELECTRIC OSCILLATOR CLOCKS
It almost never happens that a result of any considerable value is obtained at a single stroke or comes through the efforts of a single person. More often even the most important advances come as the climax of a long series of ideas which have accumulated over a period of years until the next step becomes almost self-evident and is accomplished either through the necessity for a new result or as a logical next step.
This was preeminently the case in the crystal clock development and involved the putting together of a considerable number of ideas that had been accumulating through a century or more of related activity. The chain of events which led eventually to the crystal clock followed a course quite independent of pendulum clock development, although parallel with it, and meeting it from time to time on the way. From the start, it involved the use of resonant elements whose frequencies do not depend upon gravity for controlling the frequency of oscillations in a positive feedback amplifier. From a rather simple beginning, taking advantage of a series of discoveries and inventions through about a century of progress, there has evolved a clock whose stability is comparable with that of astronomical time itself, as heretofore defined in terms of the earth's rotation, and having a versatility far exceeding all other existing means for the precision measurement of time.
The first recorded experiments that relate directly to this development were those of Jules Lissajouss8 who, in 1857, showed that a tuning fork can be sustained in vibration indefinitely by electrical means, using an electromagnet and an interrupter supported by one of the prongs. The idea of using an interrupter to sustain vibration was not new with Lissajous, but had been invented by C. G. Page9 and described by him as early as April 1837, to obtain a regularly interrupted electric current. Credit for this important invention is often given to Golding Bird10 or Neeff11 who evidently were working along similar lines concurrently although quite independently of each other. Page, Golding Bird and Neeff were all medical doctors and evidently were interested in their devices more for their therapeutic interest than for the general scientific value, since "galvanic" electricity was attributed at that time with marvelous healing powers.
Lissajous was probably the first to make use of the idea for accurate measurements of rate, being a prolific experimenter in mechanics and acoustics, and the originator of the famous method bearing his name for the study of periodic motions. Indeed, the electrically operated fork was developed especially for use as a standard to be used in studying the rates of other vibrators. In principle, the electrically operated fork is like the pendulum drive of Alexander Bain, except that the rate of vibration in this case is not a function of gravity but for the most part is controlled by the effective mass and elastic stiffness of the vibrating member.
The tuning fork itself was invented in 1711 by John Shore, a trumpeter in Handel's orchestra12, and was developed to a high state of perfection by the great instrument maker and physicist of Paris, Rudolph König. To establish an accurate standard of pitch for calibrating these forks König developed what he termed an "absolute" method for the determination of frequency. This consisted of a tuning fork having a frequency of 64 vibrations per second, with delicate mechanical means, similar to a clock escapement, for sustaining the fork in vibration and for counting the number of vibrations over any desired interval of time. For this purpose, the escapement mechanism was geared to the hands of a clock, so that when the fork had its nominal frequency the clock would keep correct time. Dr. König credits the invention of the fork-clock to N. Niaudet13 in these words:
"Cette disposition avait été realisée pour la première fois dans l'horloge à diapason que N. Niaudet fit présenter à l'Académie des Sciences le 10 décembre 1866, et que à figuré aux expositions universelles de Paris 1861 et de Vienne 1873."*
-------------------------------
* "This apparatus was realized for the first time in the fork-clock which N. Niaudet described at the Academy of Sciences on December 10, 1866, and which was shown at the expositions of the University of Paris in 1867 and the University of Vienna in 1873."
-------------------------------
Thus, as early as 1866, the essential elements had been developed separately from which a clock of the electric oscillator type could have been constructed. But it was not until more than half a century later, when there was more apparent need for such a clock, that it was actually realized. It was chiefly for the purpose of studying temperature coefficients and like properties of tuning forks that König constructed and used his famous mechanical fork-clock. There is no evidence that there was at that time any idea of using a fork-clock as a timekeeper.
It was for the purpose of making still more precise studies of the properties of tuning forks that H. M. Dadourian14 in 1919 made use of the phonic wheel motor for the first time for counting the number of cycles executed by a fork over an extended period of time to measure its rate. By means of a chronograph the time interval corresponding to the total of a very large number of periods could be measured precisely in terms of a standard clock, thus providing a direct "absolute" measure of fork rate. For this he found already invented for him all of the essential component parts, including the fork with electromagnetic drive, and the phonic wheel motor.
The phonic wheel motor, which in some modified form is an essential part of nearly all oscillator clocks, was invented by two investigators, apparently quite independently and for entirely different purposes. The first published reports of each appeared in 1878.
The first of these is an American patent that was granted on May 7, 1878 to Poul La Cour15, a Danish telegraph engineer. The application was filed in Washington on April 9 of the same year, and described a fork-controlled impulse motor similar to those still used in many modern synchronous clocks. The other publication was a report in Nature for May 23 of the March 30 Physical Society Meeting. In this, Lord Rayleigh described a motor which he developed to measure the frequency of sound by a stroboscopic method.16 Both of these original disclosures indicated a considerable amount of previous study, even including the fluid-filled flywheel to reduce hunting. It may be impossible at this time to know who actually put in motion the first phonic wheel motor.
Difficulties inherent to contact-controlled devices prevented the development of highly accurate fork standards of this type, and there is no evidence so far that any thought had been given to the use of a tuning fork as a timekeeper.
The method of using a microphone instead of a contact was proposed by A. and V. Guillet17, in 1900 and has been used considerably in frequency standards of moderate accuracy, but that too had limitations which made it impossible to utilize fully the inherent stability of a good tuning fork.
The first opportunity for really precise control of the frequency of a mechanical vibrating system, and the next step in the oscillator clock; evolution, came with the invention of the thermionic vacuum tube at the turn of the century. The development of the vacuum tube has been a more or less continuous process18 starting with the studies of electrical conduction in the neighborhood of hot bodies by Elster and Geitel, Edison, and Fleming, and later developed into the first practical devices by Fleming19 and DeForest20 in England and America respectively. The first patent for such a device, a two-element tube, was issued to J. A. Fleming in 1904.21 The first patent on a tube containing three elements and suitable for use as an amplifier was issued to Lee DeForest in 1907.22
The vacuum tube as an amplifier found almost immediate and widespread application in telephony and, next to the basic telephone elements, was the most important single factor contributing to long distance communication. For this purpose large amounts of amplification were required. Very often in the operation of early amplifiers, enough signal from the output would somehow get coupled into the input circuit to make the entire circuit break into oscillation on its own account at some frequency for which the amplifier and feedback circuit were particularly efficient.
Although this was very annoying in an amplifier, it led naturally in 1912 to the invention of the vacuum tube oscillator, consisting essentially of an amplifier with coupling between the output and the input and some definite means for regulating the frequency of oscillation. The first to seek patent protection in vacuum tube oscillators were Siegmund Strauss23 in Austria, Marconi Company in England24, A. Meissner in Germany, and Irving Langmuir, E. H. Armstrong and Lee DeForest25 in America. Many specific forms have since been invented and widely used, some of the more familiar types being associated with the names of Colpitts, Hartley and Meissner.
With the vacuum tube oscillator controlled by electric circuit elements, it would have been possible immediately to operate a clock by means of a phonic wheel motor. Even if this had been done, however, the accuracy would not have compared very favorably with that of good mechanical clocks of the period. This is because the rate-controlling element of such oscillators was subject to large changes due to temperature and aging, and because means were not yet known for avoiding the effects of tube and other variables on the resulting frequency.
The next important step in our evolution was the use of the vacuum tube to sustain the vibration of a tuning fork. This may be considered either as an improvement on the contact-driven fork by the substitution of a vacuum tube relay device instead of the contact, or as an improvement on the vacuum tube oscillator by the substitution of a mechanical resonator for the electrical resonant element. This achievement was first announced by Professor W. H. Eccles26 in April or May, 1919, and was followed on June 20 by a note by Eccles and Jordan27 in the London Electrician. Meanwhile, on June 16 of the same year, a similar announcement appeared in Comptes Rendus by Henri Abraham and Eugene Block28, showing that parallel developments were in progress in both England and France. However, Eccles and Jordan in discussing their work at the National Physical Laboratory stated: "Several instruments of this kind have been set up and used during the past 18 months." From this, we may imply that they had vacuum tube driven forks in operation early in 1918.
One of the chief advantages of the use of the vacuum tube to sustain oscillations in a mechanical system is that the variable friction of the contact mechanism is avoided. Previously this had been one of the main causes of instability. With the new method it became possible to operate in a wide frequency range, continuously, and at small amplitude, and to deliver alternating currents of approximately sine wave form and having more constant frequency than heretofore had been possible. The judicious use of a vacuum tube in delivering power to sustain the vibration of a resonator is analogous to the ideal of the so-called free pendulum but may be utilized more effectively in freeing the resonator from disturbing influences associated with the driving means.
Another important advantage, which, however, was not realized immediately, is the ease with which the phase of the driving force applied to a mechanical vibrator can be adjusted for greatest frequency stability. In a manner analogous to the pendulum, in which it was shown that the rate is least affected when the driving impulse is applied at the instant of maximum velocity, the current delivered to the driving electromagnet and hence the force applied to the vibrating element, should be in phase with the velocity of that element. In the vacuum tube oscillator, it is a relatively simple matter to design the feedback circuits to meet this condition very accurately.
In 1921 and 1922 Eckhardt, Karcher and Keiser29,30 described the development of a precise fork and vacuum tube driving means, pointing out the following uses: "As a sound source; as a small scale time standard; as a current interrupter; as a synchronizer." The chief emphasis seems to have been on the second item because in the same year Eckhardt described a high-speed oscillograph camera using the same fork as a precise timing device. The study and improvement of the tuning fork oscillator were carried on continuously and soon such oscillators were used in several national physical laboratories and commercial research institutions as standards of frequency and time interval.
The next two reports of progress appeared in 1923, one by D. W. Dye of the National Physical Laboratory in Teddington, and the other by J. W. Horton, N. H. Ricker and W. A. Marrison of Bell Telephone Laboratories, New York City. Both of these papers disclosed work done over a period of two or three years and described apparatus that had been in operation for a considerable period. Dr. Dye employed a 1000-cycle steel tuning fork and a phonic wheel motor operating synchronously from it with a gear reduction and cam to produce periodic electrical signals which he compared with a clock by means of a chronograph31. Horton, Ricker, and Marrison used a 100-cycle steel fork, a synchronous motor with a gear reduction to produce electrical impulses at one-second intervals, and a clock mechanism operating directly from these signals32. This appears to be the first time that a vacuum tube-controlled oscillator was ever used to operate a complete clock mechanism. Shortly thereafter, a clock was built in which the 100-cycle motor was geared directly to the clock mechanism instead of operating through a stepping device. A contacting device was retained, however, for the purpose of making precise time measurements.
For precise measurements of rate over long time intervals, means were provided to compare the seconds pulses controlled by the synchronous motor directly with time signals received by radio from the Naval Observatory. To facilitate these comparisons, a two-pen siphon recorder was built by means of which the time marks were laid down side by side on a moving strip of paper in such a way that accurate subdivisions of a second could be made on any part of the record.
This same two-pen recorder and 100-cycle fork time standard was used during the total solar eclipse of January 24, 1925 to time the progress of the moon's shadow as observed at a number of stations in the path which were all connected by a round-robin telegraph circuit, through the Bell Telephone Laboratories’ headquarters in New York City33,34. A photograph of the original records is reproduced in Fig. 6. This is believed to be the first time that a vacuum tube oscillator type of time standard was ever used in the service of astronomy.
Fig. 6--Timing
records of total solar eclipse of January 24, 1925.
During the following ten years a great number of improvements were made in tuning fork oscillators and they became widely used as precise frequency standards. The Bell Laboratories' 100-cycle fork standard was mounted in a container which could be sealed at constant pressure or vacuum. It was carefully temperature controlled and provision was made to keep the amplitude within prescribed limits. In describing this improved standard35, comprising a synchronous motor geared directly to a clock mechanism, the authors Horton and Marrison made the following statement:
"During tests on this frequency standard, it was found that it constituted a far more reliable timekeeper than the electrically maintained pendulum clock which was used to obtain the data already published. The pendulum clock was, therefore, dispensed with and all measurements of the rate of the fork are now made by direct comparison with the mean solar day as defined by the radio time signals sent out by the U. S. Naval Observatory."
In all fairness to the pendulum clock in question, it should be stated that the laboratory was situated on the seventh floor of a building adjoining a busy street and so was continually subject to vibration from traffic, wind, and other changing conditions. Disturbances of this sort have little or no effect on standards of the electric oscillator type but seriously impair the performance of most high precision pendulum clocks. The relative immunity of the oscillator standard to change of position and shock has an important bearing on its value in many applications.
Probably the most precise tuning fork controlled time and frequency standards ever constructed were those developed in the National Physical Laboratory at Teddington, as a continuation of the work begun there by Professor Eccles and carried forward by Dr. Dye and his staff. A report by D. W. Dye and L. Essen in the Royal Society Proceedings in 193436 described a number of refinements in the fork and method of use some of which had been suggested by Dr. Dye as a result of his studies ten years earlier. Among these was the use of elinvar in the construction of the forks in order to reduce the effect of variable temperature on the frequency. Elinvar is a nickel steel containing about twelve per cent of chromium, which on proper treatment has a small or zero temperature coefficient of elasticity. It was invented by Charles Edouard Guillaume37,38 and was further studied by P. Chevenard39,40. The excellence of the N.P.L. fork standard can be appreciated readily from the conclusion of the 1934 report which states in part:
"The frequency of the fork in comparison with the N.P.I. Shortt clock can be measured at any time with an accuracy of 5 parts in 108. It is necessary to apply a correction for the rate of the Shortt clock, and the ultimate accuracy with which the absolute value of frequency is known depends on the accuracy of the time signals which are used to determine the rate of the clock. The final frequency can, however, usually be ascertained with an accuracy of ± 1.5 parts in 107. In its present condition the turning fork maintains a frequency stability of the order of 3 parts in 107 over periods of a week or more."
A considerable amount of effort has been devoted to the improvement of tuning forks, directed mostly toward stabilizing the fork itself. Patents issued to H.H. Hagland41, August Karolus42 and Bert Eisenhour43 have been concerned with the reduction of temperature coefficient by various methods of compensation in the alloy or in the mechanical structure of the fork. In recent years, alloys have been produced from which forks with a zero coefficient of frequency can be machined. These alloys have neither a zero expansion coefficient nor a zero elastic coefficient, but the two coefficients are so balanced that their effects cancel as they concern the frequency of a tuning fork.
One of the largest residual sources of error in a good fork is that caused by the coupling through the mounting. A fork which is efficient is a producer of sound by coupling through the base would be quite useless as a precise standard of rate due to the losses introduced in this manner. It has been shown by S.E. Michaels44 that the tines of well-balanced fork can be so shaped that practically no energy at fundamental frequency is transmitted through the base.
By making use of all that is known about materials, shapes and mountings for tuning forks, and all that is known about stabilized vacuum tube circuits for driving them, it is quite possible that considerable further improvement could now be obtained in such a standard. But another line of development has shown greater promise in this field and the ultimate accuracy of tuning fork oscillators has never been pursued.
During the same ten years that the greatest advances were being made in the tuning fork art, the striking properties of the quartz crystal resonator were reviewed and first applied in the construction of frequency and time standards. Its use in primary standards for the most exacting measurements of frequency and time is now almost universal in national and industrial laboratories throughout the world.
Quartz crystal is the most abundant crystalline form of silicon dioxide, occurring, in some parts of the world, in large single crystals from which mechanical resonators of useful dimensions can readily be formed. The physical properties that make it eminently suitable for use in a standard of rate or time are its great mechanical and chemical stability. Having a hardness nearly equal to that of ruby and sapphire, and a rigidity of structure such that it cannot be deformed beyond its elastic limit without fracture, it might be expected to remain in a given shape indefinitely under ordinary conditions of use. Because of its great chemical stability, its composition is not easily modified by any ordinary environment.
In addition to its inherent physical and chemical stability, the elastic hysteresis in quartz is extremely small. For this reason, it requires only a very small amount of energy to sustain oscillation and the period is only very slightly affected by variable external conditions in the means for driving it.
A striking illustration of the importance of this property is indicated by the number of periods that a resonant element will execute freely, that is, without any sustaining forces whatever, during the time required for the amplitude to decrease to one-half of some prescribed value. For a good electrical circuit consisting of an air core inductance and an air condenser, this number is about 100; for a good tuning fork in vacuum, it is about 2000. For a good cavity resonator under standard conditions of temperature and pressure, the number may be as high as 10,000. The best gravity pendulums will swing freely from 2,000 to 20,000 times before they reach half amplitude. The effect is most striking of all in quartz crystal, in which the internal losses are extremely low. Professor Van Dyke has measured the rate of decay of oscillations under a wide range of conditions45 and has found that, as ordinarily mounted, nearly all of the losses are in the mounting or in the surrounding atmosphere, if any, or in surface effects. Extremely small amounts of surface contamination will more than double the decrement. Recently46 Maynard Waltz and K. S. Van Dyke have measured the decrement of one out of the first set of four zero coefficient ring crystals ever made47 and found that, vibrating freely in vacuum and favorably mounted, it would execute more than a million vibrations before falling to half amplitude.
The advantage of this property is immediately obvious because of the relatively small amount of energy that must be supplied at each oscillation to keep the resonator in motion. As already discussed in relation to the pendulum, the amount that the rate of oscillation may be disturbed in a given structure is proportional to this energy and, to first order, on the departure from the ideal phase condition of the applied driving force.
The properties just enumerated are sufficient to assure the superiority of quartz crystal for the control element in a rate standard; no other vibrating system known at the present time is so sharply resonant or so stable. However, one more property, its piezoelectric activity, has added greatly to the convenience of its use in vacuum tube devices.
The piezoelectric effect was discovered by the Curie brothers in 1880,48 and in the years following was studied extensively by them49,50. They found that when quartz and certain other crystals are stressed, an electric potential is induced in nearby conductors and, conversely, that when such crystals are placed in an electric field, they are deformed a small amount proportional to the strength and polarity of that field. The first of these effects is known as the direct piezoelectric effect and the latter as the inverse effect. The amount of such deformation in quartz is extremely minute, a static potential gradient of 1 esu (300 volts) per centimeter causing a maximum extension or contraction, depending on the polarity, of only 6.8 X 10-8 cm per cm. If a crystal resonator is subjected to an alternating electric field having the frequency for which the crystal is resonant, the amplitude of motion will, of course, be multiplied many times. In practice, however, the actual amplitudes of motion are kept so small, by limiting the applied electric field that even with the largest crystals used they can be observed only under a high powered microscope. This, in conjunction with means for precise amplitude control, is one of the reasons for the remarkable frequency stability of quartz crystal oscillators.
In practice, a quartz resonator is mounted between conducting electrodes which now most often consist of thin metallic coatings deposited on the surface of the crystal by evaporation, chemical deposition or other suitable means. Electrical connection is made to these coatings through leads which also support the crystal mechanically. The resonators with which we are chiefly concerned in this discussion have only two electrodes.
If such a two-terminal resonator is connected into any circuit, it will behave there as though it consisted of wholly electrical circuit elements, usually of such low loss as can not be realized by other means. The equivalent electric circuit for a quartz crystal resonator was first described51 by K. S. Van Dyke in 1925 and, for some significant cases, is illustrated in Fig. 7. The part of such an equivalent circuit which in many cases cannot be duplicated by any ordinary means is the inductance element containing so little resistance. It is as though an electric resonator could be made and utilized constructed of some supra-conducting material.
Fig.
7.--Equivalent electrical circuits for typical quartz crystal
resonators.
Among the first serious efforts to utilize the piezoelectric effect in electrical circuits were those of Alexander McLean Nicolson who used rochelle salt crystal in the construction of devices for the conversion of electrical energy into sound and vice versa. He constructed loudspeakers and microphones during several years of study prior to the publication of his work52 in 1919 - ideas now being used extensively in phonograph pickups, microphones and sound producers. Nicolson also was the first to use a piezo-active crystal to control the frequency of an oscillator. His patent53, applied for in 1918, shows a circuit which he operated successfully in 1917. The first actual use of resonators of quartz is attributed to P. Langevin54,55, who drove large crystals in resonance in order to generate high-frequency sound waves in water for submarine signaling and depth sounding.
The Quartz Crystal Controlled Oscillator
The first comprehensive study of the use of quartz crystal resonators to control the frequency of vacuum tube oscillators was made by Walter G. Cady in 1921 and published by him in April, 192256. This was the step which initiated a most extensive and intensive research of the properties of quartz crystal and into methods for its use in numerous fields requiring a stable frequency characteristic.
The extent and importance of this research are well indicated by the number of investigators and published contributions of the art. Among these, a paper by A. Scheibe57 in 1926 lists 28 articles on the subject, along with a description of his own extensive studies. Two years later Cady published a bibliography58 on the subject, including 229 separate references to papers and books and 84 patents in various countries. R. Bechmann in 1936 published a review of the quartz oscillator59 including 26 references to other original contributions in that field alone. More recently there comes at the end of Cady's 1946 book60 on "Piezoelectricity", a bibliography of 57 books and 602 separate published articles on this subject. By any measure this represents a great amount of detailed effort for a single subject in so short a time—just about a quarter of a century. Of this great amount of material, it is feasible to review only a small number of the outstanding ideas relative to the evolution of the quartz crystal clock.
The first published quartz-controlled oscillator circuit is reproduced in Fig. 8A from Cady's 1922 article. In this oscillator the "direct" and "inverse" piezoelectric effects were employed separately, making use of two separate pairs of electrodes. The output of a three-stage amplifier was used to drive a rod-shaped crystal at its natural frequency through one pair of electrodes making use of the "inverse" effect, while the input to the amplifier was provided through the "direct" effect from the other pair. The feedback to sustain oscillations in the electrical circuit could be obtained only through the vibration of the quartz rod and hence was precisely controlled by it. Cady’s results were received with widespread interest and were duplicated and continued in many laboratories, which soon resulted in many new discoveries and inventions.
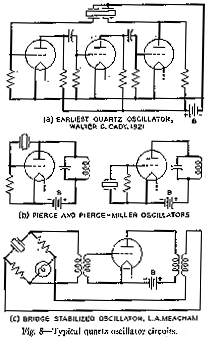
Fig. 8--Typical
quartz oscillator circuits.
Important contributions were made by G. W. Pierce, who, showed in the following year that plates of quartz cut in a certain way could be made to vibrate so as to control frequencies proportional to their thickness61. He also proposed somewhat simplified circuits for their use which soon found very general application in the construction of wavemeter standards and later for oscillators used to control the frequency of broadcasting stations and for many other purposes. In 1924, the General Radio Company of Cambridge, Massachusetts, produced a commercial instrument based on these studies.
The significance of the unusually stable properties of quartz crystal — which at times were viewed with a sort of awe and a tendency at first to expect too much62*__ was soon recognized in relation to precise standards of frequency and time, and many laboratories made experiments directed toward these applications.
--------------------------------------
*In 1929, M.G. Siadbei wrote "Nous pensons que le quartz piécoélectrique peut trouver un nouvel emploi dans la chronometrie, étant donnée la conservation rigoureusement constant de ses oscillations."
"La seul cause de variation de la période d’oscillation résulte en effect du changement de la temperature..’
--------------------------------------
For some years these efforts usually took one of two forms: either that of a quartz-controlled oscillator used as a comparison standard by various means63, or that of using the quartz resonator itself as a portable standard, the high-frequency counterpart of an isolated tuning fork. Probably the most convenient standards of the latter sort were the luminous resonators first described in 1925 by Giebe and Scheibe64. The following year they proposed the use of such luminous resonators as frequency standards65 and, shortly following, portable frequency indicators of this sort were made available for general use. The use of such a luminous resonator for the international comparison of frequency standards was reported by S. Jimbo, in 1930.66 The first international comparison of frequency standards making use of piezo resonators as isolated standards was carried out by Walter G. Cady in 1923, who by means of a set of early type resonators compared the existing standards at Rome, Livorno, Paris, Teddington, Farnborough, Washington, and Cruft Laboratory at Harvard University67. In the following year the U. S. Bureau of Standards carried out a similar international frequency comparison, but of greater accuracy, employing portable quartz crystal oscillators. This comparison and other important related studies were described by J. H. Dellinger in 1928—"The Status of Frequency Standardization"68.
It was soon recognized that quartz oscillators could be built with a stability far greater than that of any other known type and that they possess qualities very desirable for a combined time and frequency standard. However, all early quartz oscillators had frequencies far too high to operate any synchronous motor and it was not immediately obvious how a clock could be operated thereby.
The illustration in Fig. 9 from the author's notebook for November, 1924 is believed to be among the earliest means proposed to accomplish this. In brief, the proposal was to control the speed of a motor driving a high-frequency generator so that a harmonic of the generator output, say the tenth, would have a frequency of the same order as that of the crystal but differing from it by a relatively low frequency, f1. This low frequency, derived from the modulator was to be used to drive the synchronous motor.
Fig. 9—Early
suggestion of means to control a rotating device such as a clock
from a high frequency.
The shaft speed of the motor-generator would, therefore, be integrally related to the crystal frequency and hence any mechanism geared to the shaft, such as a clock, would indicate time as dictated by the crystal. This method could have been carried through readily by a combination of means already developed for other purposes, and the construction of an apparatus based on this suggestion was soon begun. However a simpler method69, not involving a rotating machine in the control system, was suggested and the first quartz crystal clock was constructed using the simpler means. This apparatus was described by Horton and Marrison70 before the International Union of Scientific Radio Telegraphy in October, 1927: The resonator in its mounting that was used in this first model is shown in Fig. 10. It consisted of a rectangular block of crystal, cut in the manner usually called X-cut, and of such size as to oscillate at a frequency of 50,000 cycles per second in the direction of its length. The temperature coefficient of this resonator was approximately 4 parts in a million per degree C at the temperature of operation, which was controlled at a value in the neighborhood of 40 degrees C.
Fig.
10--50,000-Cycle quartz resonator, in original mounting, used in
first quartz clock--1927.
The method for frequency subdivision used in this first quartz crystal clock is illustrated in Fig. 11. The inductance element of an electric circuit oscillator, designed to operate at the desired low frequency, has a core of variable permeability so that the frequency can be adjusted over a narrow range through the control of direct current in an auxiliary winding. A harmonic of this low frequency, generated in the tube following the oscillator, is compared with the incoming high frequency in the vacuum tube modulator. The harmonic chosen has nominally the same frequency as that of the control, or crystal oscillator, so that one output of the modulator is a direct current whose magnitude and sign vary with the phase relation between the inputs to the modulator. The use of this method to regulate the low-frequency oscillator insures that the low frequency is some exact simple fraction of the high frequency. If, therefore, a synchronous motor is operated from the low frequency thus produced, its rate represents accurately that of the high-frequency source as though it had been possible to use that source directly.
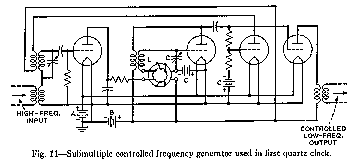
Fig.
11—Submultiple controlled frequency generator used in first quartz
clock
Several other electrical circuits were proposed around 1927 for the subdivision of high frequencies. The method in most general use at present is an adaptation of the "multivibrator" first used by Henri Abraham and Eugene Block in 1919 for the measurement of high frequencies71. They used their circuit to produce a wave rich in harmonics and having a fundamental that could be compared directly with that of a tuning fork standard. By various means now well known the high frequency could be compared with one of the harmonics of this special oscillator.
This procedure was reversed by Hull and Clapp72, who discovered that the fundamental frequency could be controlled by coupling the high-frequency source directly into the circuit of the multivibrator. This, in fact, is a general property of any oscillator in which the operating cycle involves a non-linear current-voltage characteristic, being most pronounced in those of the relaxation type. Van der Pol and Van der Mark in 1927 reported on some experiments on "frequency demultiplication" using gas tube relaxation oscillators73. The multivibrator is, in effect, a relatively stable relaxation oscillator74, and with slight modification has been used extensively as the frequency-reducing element in quartz-controlled time and frequency standards throughout the world.
One serious difficulty with the multivibrator type of submultiple generator has been that, if the input fails or falls below a critical level, it will continue to deliver an output which, of course, will not hen have the expected frequency. Certain variables in the circuit, such as tube aging, may cause a similar result. With this in view, a general method for frequency conversion has been developed by R. L. Miller75, in which the existence of an output depends directly on the presence of the control input. The basic, idea involved in this, now known as regenerative modulation, was anticipated by J. W. Horton in 191976 but had not been developed prior to Miller's investigations. The circuit of a regenerative modulator in its simplest form as a frequency divider of ratio "two" is shown in Fig. 12.
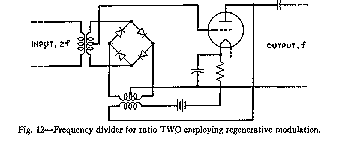
Fig.
12--Frequency divider for ratio TWO employing regenerative
modulation.
Soon after the announcement in 1927 of the first quartz crystal controlled clock,70 the idea was studied and applied in many places notably in America and Germany, and at the present time it forms the basis for precise measurements of time and frequency in many government physical laboratories as well as in many astronomical observatories and industrial and university laboratories throughout the world.
Although the first results were quite satisfying, it was the immediate interest of all concerned to find out what improvements could be made, and these were not long in coming. As in the case of the pendulum already discussed, or with any other oscillator, the constancy of rate obtainable depends on two kinds of properties: those which concern the inherent stability of the governing device itself, and those concerned with the means for sustaining it in oscillation. Some of the factors in the two groups are interrelated and must be considered together.
The improvements in quartz oscillator stability therefore have been concerned with two main endeavors, namely that of cutting and mounting the resonator so as to realize effectively the unusually stable properties of quartz crystal itself, and that of coupling it to the electrical circuit in such a way as to avoid the effects of such variables as power voltage variation, aging of vacuum tubes, and the like, on the controlled frequency. The latter effects were not obvious at first because the temperature coefficient and the effects of friction and change of position in the mounting caused variations of considerably larger magnitude. It was natural, then, to see what could be done about these effects.
Zero Temperature Coefficient of Frequency
With the knowledge that X-cut resonators had negative coefficients, frequently as large as thirty parts in a million per degree C, and that Y-cut resonators in general had positive coefficients, often in excess of a hundred parts in a million per degree, the author undertook to make resonators of such shape that the oscillations would occur in both modes simultaneously, and so combine the coefficients, in the hope that the resultant could be made zero.77
The first experiments, made on two series of resonators both yielded encouraging results. The first was a series of rectangular X-cut plates of varying thickness shown in Fig. 13. The second was a series of three circular discs of different diameters, all being cut with the large surfaces in the plane of the Y and Z axes. The three discs were made from the same material, each smaller one being trepanned from the previous one after complete measurements had been made upon it. The set of circular crystals remaining after these tests were completed is shown in Fig. 14 and the slab from which they were cut is shown assembled with the original large crystal in Fig. 15.
Fig. 13--Set
of rectangular quartz resonators made for zero temperature
coefficient study.
Fig.
14--Circular pieces remaining after temperature coefficient study of
quartz discs and rings.
Fig. 15--Large
crystal and slab from which low coefficient studies were
made.
Subsequent tests showed that the annular pieces could be designed for a low or zero coefficient and such a shape shown in Fig. 16 was employed for a number of years in the Bell System Frequency Standard in New York City78. As described in this reference, the reason for using the ring in preference to the solid disc or rectangular plate was in the convenience of mounting. The rings were formed with a ridge in the central plane of the hole so that they could be supported on a horizontal pin thus providing a one-point support at a position where the vibration is very small. The rings used in this first application of zero coefficient quartz resonators have been called "doughnut" crystals for obvious reasons. In Fig. 17, George Hecht is shown making a final adjustment, by "lapping" with fine abrasive, on one of the four original zero-coefficient ring crystals. Mr. Hecht made all four of these resonators, as well as many others of various shapes and sizes used in the early experiments in this work.
Fig.
16--100-Kilocycle quartz ring resonator with zero temperature
coefficient.
Fig.
17--George Hecht finishing the first set of zero-coefficient quartz
rings.
Supported as described, the rings hang in a vertical plane and, as first used, they were supported freely between solid electrodes rather closely spaced to the flat surfaces. The small amount of free motion relative to the electrodes, inherent in this sort of mounting, caused occasional changes in frequency if the support were disturbed, which at times would be as large as one part in ten million. To avoid this difficulty, other ring crystals were constructed with a sort of narrow shelf at the central plane that could be mounted in a horizontal plane on pin supports. The two methods of supporting the ring resonators are illustrated in Fig. 18. Such resonators were used in the Bell System Frequency Standard until 1937 when they were replaced by an entirely different type that will be described later.
Fig.
18--Methods of mounting quartz ring resonators.
The rings were adjusted to oscillate at 100,000 vibrations per second, the frequency which has been adopted in nearly all oscillators of extremely constant rate. All of these rings were constructed to have a zero frequency temperature coefficient at a temperature in the neighborhood of 40 degrees C, the frequency being a maximum at that point on an approximately parabolic characteristic. The zero temperature coefficient makes it possible to practically eliminate frequency changes caused by ambient temperature changes since, by relatively simple means, it is possible to control the resonator within ± 0.01 degree C, at the temperature for which the effect is substantially nil. The reduction of the effect of temperature, and the stabilization of the mounting, increased the stability of frequency control and oscillator-clock rate beyond anything that had ever been obtained before. Subsequent improvements that will be described later produced even greater stability.
The striking stability of the crystal oscillator clock led the author to propose the general use of this type of clock for precision timekeeping, the chief emphasis having been previously on the derivation of constant frequency. A paper entitled "The Crystal Clock,"79 presented before the National Academy of Sciences in April, 1930, described such a clock and pointed out some of its properties and likely uses.
Chief among these properties, of course, is its inherent stability and relative freedom from extraneous effects. The quartz crystal clock is not dependent on gravity and, without any compensating adjustment, will operate at the same rate in any latitude and at any altitude. This property already has been useful in the measurement of gravity and gravity gradient by measuring the rates of pendulums on land and at sea.80,81
The crystal clock is practically immune to variations in level and shock and can be used as, an instrument of precision under conditions entirely unsuitable to pendulum clocks. For this reason it performs satisfactorily in practically any location, including earthquake zones, and may be used in transit as in a submarine, in an airplane or on the railroad.
Some of the outstanding properties of the quartz oscillator clock were discussed in 1932 by A. L. Loomis and W. A. Marrison82, in relation to a series of experiments comparing the performance of quartz clocks at Bell Telephone Laboratories in New York and a set of synchronome free-pendulum clocks operating in the Loomis Laboratory in Tuxedo Park, about fifty miles away. The comparison was effected through a circuit maintained between the two laboratories over which a 1,000-cycle current controlled by a crystal in New York was used to drive the Loomis Chronograph83 in Tuxedo Park. During part of the time, signals from the clocks were sent back over the same circuit and recorded on the Bell Laboratories' Spark Chronograph84.
The quartz oscillator assembly at the Bell Telephone Laboratories at the time of these experiments is shown in Fig. 19. The four ring crystals in their individual temperature-controlled 'ovens' are mounted under hermetically sealed bell jars to avoid the effects of ambient temperature and atmospheric pressure changes. The vacuum tube oscillator circuits are immediately below the bell jars; and the control, monitoring and power supply equipment in the remainder of the space.
Fig. 19 - Bell
System Frequency Standard, 1930.
One of the most interesting results of these cooperative experiments was the measurement of a periodic variation in the rate of the pendulum clocks in phase with the lunar daily cycle. The amount of this daily variation is very small, being only a few tenths of a millisecond, but readily observable in comparison with a stable rate standard that does not vary with gravity.
Further Refinements in Quartz Clocks
The spectacular results from the use of the quartz crystal clock up to this time, about 1932, were due in part to its novelty and in part to the fact that it is quite independent of some of the variable factors that affect conventional precision clocks, including gravity itself upon which the rate of all pendulum clocks depends. The remarkable stability of present day quartz oscillators and clocks is the result of a series of developments and refinements extending over a number of years.
As mentioned previously, the factors that cause departure from constant rate in the completed operating device fall into two distinct classes, namely those which concern the inherent or natural frequency of the resonator itself, and those which concern the means for driving it at that inherent rate.
The first class comprises all those properties of the mounted resonator which tend to relate its inherent rate to ambient conditions such as temperature, atmospheric pressure, change of position and vibration, and to the passage of time—that is, aging. Since the final stability cannot exceed the inherent stability of the mounted resonator itself, its study is of prime importance.
The second class comprises properties of the means for sustaining oscillations in such a resonator which relate the resulting actual rate to variations in the electrical circuits, in the power voltages, in vacuum tubes and other like effects. In the limit, it is the hope that the net result of all such effects can be eliminated so that the stability of the quartz crystal alone will remain the sole governing factor. This is the goal, and the inherent stability of the substance, quartz crystal, is the limit toward which the stability of the quartz crystal clock will approach but cannot exceed.
The development of the quartz resonator and its mounting for numerous applications is described in some detail by Raymond A. Heising and his collaborators85 in their recent book, "Quartz Crystals for Electrical Circuits". Of all the types of resonator described in this work the one having the most extensive use at the present time, for quartz clock installations and for other applications of comparable accuracy, is the GT crystal resonator developed by W. P. Mason86. This resonator is cut from quartz crystal in such a way that the positive and negative coefficients are effectively neutralized over a range of about 100 degrees C, so that in any part of this range the resulting temperature coefficient of frequency is not more than one part in a million per degree C. With suitable precautions in manufacture, the tangent at the point of inflection in the frequency-temperature curve may be made horizontal, which means that the temperature coefficient may be made substantially zero over a considerable range of temperature.
The GT crystal resonator therefore introduces two significant advantages in timekeeping, namely that greater accuracy of rate may be obtained with a given accuracy of temperature control arid that the value at which the temperature is controlled may be chosen in a considerable range. In fact, without any temperature control at all, the rate of a clock regulated by such a crystal may be accurate to a tenth of a second a day over an ambient range of 100 degrees C. Among the many quartz clock installations now using the GT resonator; all or in part, are the Royal Observatory at Greenwich, the British Post Office, the U. S. Naval Observatory and the U.S. Bureau of Standards.
One of the chief sources of variation in rate of quartz oscillators, in the early stages of their development, was in the means for mounting and in the electrical circuit connections. As mentioned previously any variation in the effective resistance or in the effective mass or stiffness of a resonator has a direct effect upon its rate of oscillation. The problem reduces to that of supporting the resonator so that the frictional losses are small and constant and so that the coupling to the electrical circuit is as nearly as possible invariable.
The mounting of quartz crystal units is
discussed at length by R. M. C. Greenidge in Chapter XIII of Mr.
Heising's book referred to above.85 The most satisfactory
means by far that has been found for mounting crystals of the GT
type is that of actually soldering them to thin supporting wires by
means of small discs of silver deposited on the crystal at its
nodes. This method serves the double role of supporting the crystal
and of providing electrical connection to metal electrodes plated on
the crystal. Resonators so supported may be made almost immune to
mechanical shock and will continue in satisfactory operation through
accelerations of several times 
. Nearly all crystals
which vibrate in a long dimension are now mounted in this way. One
manufacturer produced about 10,000,000 crystals of a single type so
mounted in a three-year period during World War II. Prior to the use
of wire supports, such crystals were "pressure mounted" by means of
small metal jaws which clamped from opposite sides at the nodes. A
GT crystal mounted in this way is shown in Fig. 20. Crystals so
mounted are still in use in the Bell System Frequency Standard,
being the first of the GT crystals to go into actual service. This
type of mounting is not quite so stable as the wire mounting and is
somewhat more difficult to manufacture. One of the wire-mounted
crystals such as developed for LORAN and other Oscillators of
comparable accuracy is shown in Fig. 21.
Fig.
20—Pressure-mounted GT crystal for sealing in a metal
envelope.
Fig.
21—Wire-supported GT crystal sealed in a glass envelope.
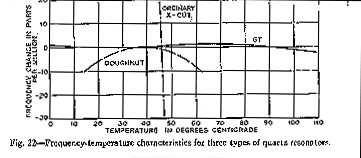
Fig.
22—Frequency-temperature characteristics for three types of quartz
resonators.
The plating of electrodes on the crystal surface has led to increased stability of frequency control, chiefly because the coupling to the electrical circuit may be kept more nearly constant thereby. When separate electrodes were employed, the variation in spacing was always found to be a source of instability, as mentioned previously in relation to the use of the first ring crystals. Plating of crystals is not a new idea but the application to quartz resonators of high Q requires a great amount of technical skill in order to obtain coatings which are mechanically and chemically stable and which utilize the minimum of added material. The use of too much metal will, of course, impair the resonator by increasing its rate of energy dissipation and probably its aging rate. The metal most often used for electrodes is silver, although gold and aluminum have been used in special cases. Evaporation in vacuum has been found to be the most satisfactory method for the actual plating, giving very adherent coatings and being subject to precise manufacturing control. The art of plating quartz resonators is discussed in detail by H. W. Weinhart and H. G. Wehe in Mr. Heising's book.
Several other factors have had an important bearing on the final stability of quartz resonators. One of the most important of these is the care that must be exercised during fabrication in order to avoid setting up stresses in the material that subsequently can be relieved only slowly. By slow grinding with adequately fine abrasive such effects can be kept very small. Etching with hydrofluoric acid has resulted in much further improve melt through the removal of stressed surface material and all potentially loose material which, formerly, often caused anomalous aging effects. Artificial aging by heating, and thorough cleaning before and after plating, have also contributed greatly to the final stability of the crystal unit. The resonator finally is mounted in high vacuum in a glass envelope in order to eliminate losses due to sound radiation and friction, and to protect it from surface contamination and chemical action.
Even the most perfect quartz resonator, in an ideal mounting, is unable to keep time unless it is maintained in oscillation; and, like a pendulum, its rate will depend in large part on the manner in which it is driven. The same general principles apply to both cases, except that usually a pendulum is driven by impulses which should be applied when the velocity is maximum, while a quartz resonator is usually driven by a sinusoidal force arising through the piezoelectric coupling, and so phased that the maximum force occurs when the velocity is maximum. This, in fact, is a required condition for maximum rate stability. The graphical analysis of Fig. 5 applies equally for the case of sine wave drive, since the sine wave can be considered as the summation of an impulse at its peak and of sets of pairs of impulses symmetrically disposed with respect to it. Obviously, the phase errors for each such pair of impulses cancel, bringing us back to Airy's condition, but with the broader view that, for the feedback or driving wave to have minimum effect on the rate of an oscillator, the force wave must be in phase with the velocity of the resonator.
Numerous vacuum tube circuits have been proposed and used for maintaining quartz resonators in oscillation, some of which are illustrated in Fig. 8. The one among these which at present most nearly approaches the ideal is that developed by L. A. Meacham, known as the Bridge Stabilized Oscillator.87 This oscillator, in its original form or with slight modifications, is now used almost universally in England and America where the maximum stability of rate control is required.
In the bridge stabilized oscillator, the feedback path is through a Wheatstone bridge with the crystal in one arm and with resistances in the other three. The frequency of oscillation becomes that for which the reactance of the crystal approaches zero; the bridge can only be balanced when the crystal behaves electrically like a resistance. The unbalance voltage from the bridge is fed back into the amplifier, which should provide a relatively high gain, as will appear. The great frequency stability of this oscillator depends upon the fact that, in the neighborhood of balance, a small phase shift in the resonant elements causes an enormously larger phase shift in the unbalance voltage. But the actual amount of this unbalance phase shift is limited by the fact that it must be equal and opposite to that in the amplifier in order for oscillations to be sustained. This insures that at all times the phase shift in the crystal is much smaller than that occurring in the amplifier which itself can be made small by suitable design. The ratio of the phase shift of the bridge output to that of its input increases as balance is approached, making it possible to practically eliminate the effect of phase shift in the amplifier simply by increasing the amplifier gain. Most of the variable factors in the amplifier of an oscillator circuit affect the controlled frequency through the phase shifts caused by them. It is evident, then, that the bridge circuit, which permits only a small fraction of such phase shifts to become effective at the resonant element, will substantially free the resonator from variable effects in the amplifier and allow it to control a rate determined almost wholly by its own properties.
When the above condition is attained and the crystal resonator, when oscillating, acts in the circuit like an electrical resistance, it acts that way because the velocity is in phase with the applied mechanical force, which, as has been stated, is the condition for most stable rate control. In the crystal oscillator, this ideal condition is obtained simply by the automatic balancing of a bridge circuit, accomplishing in a most elegant manner the equivalent, in the case of a pendulum, of applying driving pulses at the exact center of swing.
The bridge-stabilized oscillator includes also an automatic control of amplitude. The variation of frequency with amplitude is very small and in no way comparable with the "circular error" of an ordinary pendulum, but in the quest for the highest attainable stability it must be taken into account.
The control of amplitude is obtained by the use of a resistance with positive temperature coefficient in the bridge arm conjugate to the crystal, chosen so as to have exactly the right value to balance the resistance of the crystal when a specified current is flowing in the bridge. If larger than normal current flows momentarily the resistance is increased, which decreases the feedback, thus stabilizing the amplitude at some predetermined value. For the highest stability it has been found advantageous to operate the crystal at a very small fraction of the amplitude that normally would be used in a power oscillator. In power oscillators the crystal sometimes is subjected to strains near .the fracture point, which is not a favorable condition for precision control. The actual amplitude of motion of the crystal is of course extremely small. In the GT crystal, as currently used, the maximum change of dimensions during oscillation amounts to only about +0.0006 per cent.
The improvements in quartz resonators, and in their driving circuits, have resulted in the construction of quartz crystal clocks that will keep time with an accuracy better than 0.001 second a day, so that measurements of time of great interest and value to astronomers and geophysicists can now be made with an accuracy hitherto unattainable.
Facility of Precise Time Measurement
In making such precise measurements of time it is of importance, second only to the inherent accuracy of the standards themselves, to have available means whereby they can be carried out with facility and within a reasonable time interval. The ease with which precise time measurements, and precise rate comparisons, can be made is an outstanding feature of the quartz crystal clock and already has an important bearing on the use of this type of clock in astronomical observatories. This facility depends chiefly on two properties of the oscillator clock: first, that continuous rotation of controlling and measuring devices can be produced having the stability of the primary control element; and, second, that the period of the control element, and therefore of alternating current controlled by it, is of very short duration.
The first of these, through simple devices controlled directly from the electrical output of the crystal oscillator, with suitable frequency reducing equipment, permits of ready comparison between any time phenomena in the form of electric or light signals, and of the derivation of precisely controlled time signals for radio transmission and for laboratory experiments.
Of prime importance among these comes the means for rating crystal clocks in terms of stellar observations using meridian transits or the photographic zenith tube88. It is possible to control a mechanism in the time-star observing equipment so that the difference between a star position predicted from the clock rate, and the actual star position, can be observed directly or recorded photographically with great accuracy. The difference thus observed, after allowing as well as possible for known systematic errors, is the best known single check on the time indication of a clock. A series of such observations constitutes the best known measure of the rate of a clock. The great value of the method is that the comparisons are made directly without the need of any intermediate mechanism thus eliminating a large part of the "personal error" of observation. The probable error of observation as derived from a number of such measurements on a good night may be as small as one or two milliseconds89. The average rate of a clock thus determined depends on the number of days over which the rate is computed and in a two-week period may be compared with the rate of the earth, that is, with astronomical time, with an accuracy of one part in one hundred million or about a third of a second a year. All this, of course, is contingent on the stability of the quartz clock, which, except for long-time effects, may be demonstrated independently.
A rotating mechanism controlled directly from a crystal clock is admirably adaptable to the transmission of precise time signals. Rhythmic signals of any desired structure can be produced readily by means of cams, special generators, or interrupted light beams, and the timing of those signals can be adjusted as precisely as the clock time is known by simply advancing or retarding the signal generators. Such adjustment is attained readily by means of differential gearing in the mechanical system, or by means of continuous phase shifters in the electrical driving circuit. The use of electrical phase shifters for this purpose was first proposed in "The Crystal Clock" paper79 previously mentioned. Figure 23, taken from that paper, illustrates the manner of using the phase shifter with one type of time signal generator. Extremely fine control of timing is possible by rneans of the electrical phase shifter since it can he included in the circuit at any stage of frequency subdivision. If, for example, it is used at the lowest frequency, assumed to be 1,000 cycles, one complete turn of the phase shifter dial will cause a progressive time adjustment of one millisecond. When used at a higher frequency, the precision of adjustment is increased correspondingly. Continuous phase shifters suitable for such purposes were proposed as early as 1925.90 The idea of utilizing continuous phase shifters for the purpose of making controllable changes in the frequency or indicated time in a standard time and frequency system91 was first disclosed in a comprehensive patent filed in 1934 and issued to Warren A. Marrison in 1937. The most elegant type of phase shifting element suitable for such purposes was developed by Larned A. Meacham.92 This has been used in many transmission systems requiring continuous variation of phase such as in variable direction radio beam systems93 and LORAN.
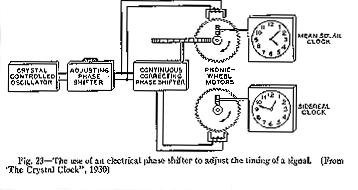
Fig. 23--The
use of an electrical phase shifter to adjust the timing of a signal.
(From "The Crystal Clock", 1930)
The conversion between mean solar time and sidereal time, or for that matter between any time systems, may be accomplished very easily with the quartz clock. Having a rotating device, such as a dial or commutator, whose rate corresponds to mean solar time, it is only necessary to apply a gearing or the equivalent to obtain another rate corresponding to sidereal time. It has been shown by F. Hope-Jones94, Ernest Esclangon95 and others how any desired ratio, such as the ratio of the rates of mean solar and sidereal clocks, can be obtained with any required accuracy by gearing. A combined mechanical and electrical method was proposed in the "Crystal Clock" paper by means of which this ratio can be realized with an accuracy of one part in 1011 using simple gearing and a continuous phase shifter.
The potential value of the factors just (discussed in precision time studies was realized early in the crystal clock development. This was indicated in the "Crystal Clock" paper written in 1930 which closed with the following paragraph:
"It would thus be possible to combine, in a single system mean solar and sidereal time indicating mechanisms, means for rating the clocks in terms of time star observations and means for transmitting time and frequency signals with the absolute accuracy of the time determinations."
It is of some interest to compare this predication with the present trend of development. In describing the quartz clock installation in the Royal Observatory in Greenwich, Sir Harold Spencer Jones stated89 in 1945:
"The quartz clocks being installed at the Royal Observatory are all adjusted to give a frequency of approximately 100,000 per mean time second. By suitable gearing, the synchronous motor can give impulses every sidereal second and tenths of a second. Thus, the same clock can be made to serve both as a mean time and as a sidereal time standard. All time signals are, of course, sent out according to mean time; the sidereal time is required only for the actual time determination so that it is not necessary for all the clocks to have the gearing to give sidereal seconds."
The importance of the convenient methods for measuring time and time interval inherent to the crystal clock is emphasized by the fact that some observatories employed crystal clock mechanisms in connection with stellar observations and in the transmission of time signals before they were used in the actual time keeping department88.
The second property contributing greatly to the convenience of precise time measurements is the relatively very short period of the quartz clock control element. The chief advantage lies in the extreme accuracy with which the rates and indicated times can be compared by electrical methods. An example will suffice to illustrate this point. Since the rate of a crystal clock is the rate of oscillation of the crystal or of the current driving it, it is only necessary, in comparing clock rates, to measure the relative frequencies of the oscillators concerned. This can he done by any of the standard methods for frequency comparison96 but, in the case of quartz clocks, since in general the primary frequencies are high and are nominally the same, special methods of extreme accuracy can be employed. The apparatus first designed for the ultra-precise comparison of quartz oscillators and capable of an accuracy of one part in 1010 was described by Marrison in 1929.78, 97, 98. The principle of its operation is shown in Fig. 24, reproduced from the paper "High Precision Standard of Frequency".
Fig.
24--Device for comparison of oscillator rates accurate to 1 part in
10,000,000,000. (From "High Precision Standard of Frequency",
1929.)
Two oscillators to be compared were adjusted so as to differ by about one cycle in ten seconds. The problem reduces to that of measuring the beat frequency, nominally 0.1 cycle per second, with as great accuracy as possible. This was done by measuring the duration of each beat by a photographic method. By means of a modulator, a relay, and induction coil, a spark was produced at the spark gap at a definite phase of each beat period. The spark illuminated the edge of a transparent scale rotating 10 revolutions per second under control of one of the oscillators, O1. The transparent scale contained 100 numbered divisions, which therefore represented milliseconds in any time interval so measured. Each time a spark occurred, the portion of scale illuminated was registered on photographic film. Thus, the duration of each beat was registered photographically with an accuracy of one part in ten thousand. Since the beat frequency is one millionth of the high frequency, the resulting comparison of high frequencies is precise to one part in ten thousand million, or 1 in 1010. Actually, it was possible to estimate fractions of a scale division which gave greater precision of measurement than was required in the study of oscillators of that date.
L. A. Meacham in 1940 improved upon this method of frequency comparison by substituting an electronic relay for the mechanical relay, and by using a discharge lamp instead of a spark for illumination. He used the improved apparatus99 for studying the behavior of the then new and highly stable bridge stabilized oscillators.
Still further improvements in the general method have been reported by H. B. Law using a "phase discriminator" to trigger off a special chronometer, consisting of a decimal scaling counter, and thus avoiding the photographic process100. The scaling counter as used here counts the number of cycles of a 100,000-cycle input timing wave that occur during any one beat between the two frequencies being compared, and registers that number, in scale of ten, on a system of dials that can be read directly. In comparing frequencies that are free from interference, the accuracy of comparison by this means is limited chiefly by the precision with which the "phase discriminator" can mark the beginning of successive beats. An accuracy of one part in 1011 is claimed. This is one of the rate comparison means employed in the frequency and time standards of the British Post Office and in measurements involving the quartz clocks of Greenwich Observatory and the National Physical Laboratory.
The scaling counter is a particularly useful device for the precise measurement of any time or rate phenomena that can be reduced to the measurement of short time intervals. The counter idea originated some years ago as a means for counting alpha-particles and other phenomena associated with radioactivity studies, one of the original devices being the well known Geiger-Muller counter. The basic scaling circuit, used in many counters, was proposed in 1919 by W. H. Eccles and F. W. Jordan. An interesting history of counting circuits as applied primarily to the counting of electron and nuclear particles has been written by Serge A. Korff in his book on that subject published in 1946.101 The early scaling circuits operated on the binary system, but recently various circuits have been developed that give the count in scale-of-ten notation with certain advantages, chiefly that of convenience, associated with the common decimal system of notation. A discussion of some modern binary and decade electronic counters102 was published by I. E. Grosdoff in September, 1946.
Methods of measurement such as this, and the stable properties of the quartz clock which make them desirable, are of importance in the precise measurement of time because the nature of variations in rate, so small that, if continued unchanged they would accumulate to only one second in a thousand years, may be studied under controlled conditions in the laboratory, and with such facility that a comparison with this precision can be made every ten seconds.
In a simpler manner, the short period of one oscillation of the quartz oscillator is of direct interest to the astronomer in connection with means for the intercomparison of his clocks in time. This reduces simply to counting the number of cycles gained or lost by one oscillator, referred to another, and may be accomplished in a great number of ways, yielding, on the basis of whole numbers of cycles, an absolute accuracy of time comparison of 0.00001 second.
An elegant method for accomplishing this103, which also indicates automatically which clock is fast or slow, employs a special vacuum tube circuit to produce a polyphase current having the frequency however small of the difference between any two oscillators nominally the same. This polyphase current is used to operate a special synchronous motor whose angular position corresponds at all times to the phase angle of the vector representing the polyphase current. This relation holds all the way to zero frequency difference, in which condition the angular position of the motor, now at rest, indicates the phase relation between the two high frequencies. If the beat frequency goes through zero, the motor reverses. By this means, it is possible with very simple equipment to set up dial indicators showing continuously the time comparisons between any group of quartz clocks, taken in pairs, with an absolute accuracy of 0.0001 second. Of course, to operate other indicators, contacts, etc. from this device is a simple mechanical problem.
The principle of operation of the polyphase modulator is illustrated in Fig. 25, which shows one of the many possible forms of this device. Other modulator elements than vacuum tubes are used in some applications. In the form shown here it is necessary only to assume that the vacuum tubes produce second-order modulation, the lowest-frequency component of which is employed. If inputs at the two frequencies ƒ1 and ƒ2, which are nearly the same. are delivered into the two balanced modulators A and B in such a way that there is a 90-degree phase shift between the two input voltages for one of the frequencies, the lowest-frequency component appears as a sinusoidal current in the output circuits 1, 2, 3 and 4 separated in phase by 90 electrical degrees in cyclic rotation. The principal output, therefore, is a 4-phase current having the frequency of the difference between the two inputs. If the magnetic circuits are arranged geometrically as shown, the resulting magnetic vector will rotate clockwise or counterclockwise depending on which frequency is high, or will remain stationary, indicating the phase relation, if the two frequencies are exactly equal.
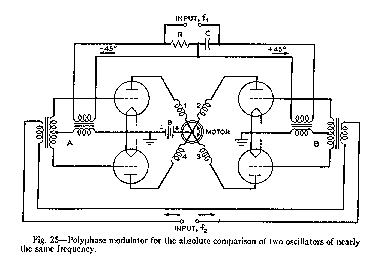
Fig.
25--Polyphase modulator for the absolute comparison of two
oscillators of nearly the same frequency.
Motors have been designed and are commercially available suitable for operating synchronously from such polyphase modulators, and form an excellent basis for the intercomparison of quartz oscillators and clocks with ultra-high precision.
For making records of time comparisons the spark chronograph84 shown in Figs. 26 and 27 has served a very useful purpose, combining in a single convenient instrument the means for comparing recurrent time phenomena with an accuracy of a millisecond or two on a continuous chart which shows the records for an entire week. Electrical impulses, related to the time phenomena to be recorded, operate trigger tubes which discharge condensers through the primary of an induction coil and cause sparks to jump from a rotating spiral through a special chart paper having a dark colored backing and coated with a very thin layer of white wax. As the chart paper moves slowly under the spiral, corresponding to the time abscissa, the succession of sparks produces readily visible traces consisting of rows of tiny holes with small areas around them where the wax is melted revealing the dark background. The holes are so small as to be scarcely visible, the darkened areas constituting the visible trace. Figure 28 shows an enlargement of the record of a single spark illustrating the nature of the marking. A recorder104 very much like the Bell Laboratories' spark chronograph is used currently as part of the standard frequency and time broadcast equipment of the U. S. Bureau of Standards.
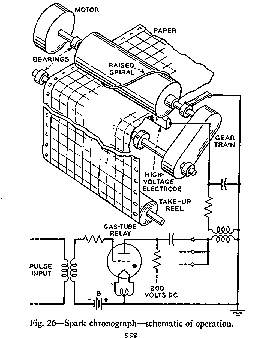
Fig. 26--Spark
chronograph--schematic of operation.
Fig. 27—Spark
chronograph—close view of mechanism.
Fig.
28--Photomicrograph of single spark record showing nature of
recording on wax-coated chart paper. X100
The many useful properties of the quartz crystal clock have been the reason for its wide and expanding application for the precise measurement of time and rate.
First in historical order was the application to the measurement and control of frequency in communication. In this, the clock, through comparisons with astronomical time, served as the means for determining the frequency controlling it, the stability from the outset being great enough over intervals of a day or more so that the average rate, as determined by daily checks with time signals, was a very close approximation to the instantaneous rate at any time intervening. The first of these clocks, already referred to70, was constructed in 1927 at the Bell Telephone Laboratories, in New York City, primarily for use as an accurate standard of frequency. Since that first experiment, three subsequent installations have been built in replacement with progressively improved performance. The standard now in operation (1947) was installed in 1937, using the first laboratory model GT crystals and the first set of four bridge-stabilized oscillators, and has been in operation continuously since that time. Two of the four oscillators, mounted in a temperature controlled booth, are shown in Fig. 29, and part of the auxiliary equipment, including a clock dial, a spark chronograph and some monitoring equipment, is shown in Fig. 30. This apparatus serves as the standard for precise measurements of frequency and time throughout the Bell System and is used to regulate the telephone Time of Day Service in New York City. It is the standard of reference for the electric light and power services in Metropolitan New York105, and is used for a number of other similar services, distributed through the medium of a submaster installation106 maintained by the Long Lines Department of the American Telephone and Telegraph Company. The original oscillators in this submaster installation were controlled by electrostatically-coupled 4000-cycle steel tuning forks in vacuo but recently have been replaced by improved oscillators controlled by 4000-cycle bi-morph quartz resonators.
Fig. 29--Two
of the four quartz oscillators of the Bell System Frequency
Standard, 1937 to date.
Fig.
30--Clock dial and monitoring equipment associated with the Bell
System Frequency Standard, 1937 to date.
A clock shown in Fig. 31, which is on display in a window of the American Telephone and Telegraph Company at 195 Broadway, is controlled from this source. It is sometimes called "The World's Most Accurate Public Clock".
Fig.
31--Display clock at 195 Broadway, New York. This clock, controlled
by the Bell System Frequency Standard, shows the same time as that
of the New York Telephone Time Service.
The facility with which standard frequency and time services can be provided and distributed is an outstanding feature of the quartz clock development. Such services, having the accuracy of the primary controlling standard, may be provided anywhere that can be reached through a suitable communication channel. As an example of this, a new primary standard equipment is being constructed for installation at the Murray Hill, New Jersey location of Bell Telephone Laboratories, the services of which will be made available through permanent wiring to all departments concerned. A number of frequencies in the range from 60 to 10,000,000 cycles, all controlled from the same crystal source, will be made available at some thirty locations at the Murray Hill Laboratories, as well as to other laboratories of the Bell System and, through the Long Lines Department, to outside agencies.
A considerable number of quartz clocks have been built and used in laboratories and observatories all over the world, some as standards of frequency, some as precise clocks, and others for general use in all measurements of rate and time. It would be impossible to mention all of these, for already there are many of them. But certain installations are of especial interest and will be discussed briefly.
When the Crystal Clock was first described as such in April 1930, the idea was discussed quite widely in Europe and America, and it was not long before the work was duplicated and extended in other places. The first outstanding application of the quartz clock to astronomy was made in Germany with the installation at the Physikalisch-Technische Reichsanstalt. This was described by Scheibe and Adelsberger in 1932107 and 1934108, and reports of its splendid performance continued periodically. It was with this installation that it was possible for the first time to observe and measure variations in the earth's rate occurring over intervals as short as a few weeks. Previous measurements of such variations, involving studies of motion of the moon, the planets, and Jupiter's satellites, had required years to obtain comparable information which, of course, by nature, could never reveal short-term factors.
Soon after the inauguration of the quartz clocks at the Physikalisch-Technische Reichsanstalt, somewhat similar installations were made at the Prussian Geodetic Institute at Potsdam109, and at the Deutsche Seewarte in Hamburg110. The latter has been moved because of war conditions and is now the Deutsche Hydrographische Institut. The quartz resonators used in these installations are believed to be similar to those in Clocks III and IV in the Physikalisch-Technische Reichsanstalt installation except that some of them were made for 100 kilocycles instead of the original 60 kilocycles. They were made by the firm Rohde and Schwarz where also is maintained a quartz clock installation of extremely high precision111.
For a number of years the U. S. Bureau of Standards at Washington, D.C. has maintained a quartz clock installation for their extensive constant frequency and time services. The early history of' this installation was described in some detail by E. L. Hall, V. E. Heaton and E. G. Clapham in 1935.112 As is now well known, the Bureau broadcasts a number of precisely controlled carrier frequencies at all times, all of which carry standard time and frequency modulations, including audible pitch standards and time signals. The audible pitch standards are 4000 cycles and 440 cycles, while the time signals consist of a succession of seconds pulses, continuous except for certain omissions for the purpose of identifying longer time intervals. All of these rates, including the carrier frequencies, are derived directly from crystal oscillators and are known so well that their accuracy as transmitted is estimated as one part in 50,000,000 at all times. The relative rates of the standard oscillators are compared and recorded continuously at the Bureau of Standards with an accuracy of one part in 109. The time signals involved in these transmissions are so precise, and so convenient to use, that they may be employed for the high-precision intercomparison of quartz clocks across the Atlantic and for studies in astronomical time, heretofore difficult or impossible to accomplish by any other means.
The present standard frequency and time service facilities at the U. S. Bureau of Standards, which have been instituted under the general direction of J. H. Dellinger, are described in recent separate articles113, 114 by Vincent E. Heaton and W. D. George respectively of the Bureau, both of whom have made very substantial contributions to this development. The transmitting station for the standard frequency broadcasts, which comprises a complete set of quartz oscillators and control and measuring equipment, is shown in Fig. 32.
Fig. 32 - WWV
- The Standard Frequency Broadcasting Station of the U.S. Bureau of
Standards.
The absolute rates for the crystal oscillators at the Bureau of Standards are determined through cooperation with the U. S. Naval Observatory, also at Washington, where time determinations of great accuracy are made by means of a Photographic Zenith Tube and a set of quartz clocks. A continuous precise check is maintained between these organizations by radio communication so that the Naval Observatory time signals sent out from NSS at Annapolis and other Navy stations, and from WWV the Bureau of Standards radio transmitting station at Beltsville, MD., as well as all the carrier frequencies from Beltsville, are very accurately determined and maintained in agreement throughout.
The time studies of the U. S. Naval Observatory up to 1931 are described in two important articles by J. F. Hellweg, then Superintendent of the Observatory. The first of these115 in 1932 describes the state of the art just before the quartz clock entered the scene, and the second88 in 1937, already referred to, tells of some of the first improvements brought about by its use including the elegant method for making direct photographic time-star checks of the crystal clock rate by means of the Photographic Zenith Tube. Many of the advances involving the use of quartz clocks at the Naval Observatory have not as yet been published.
The British Post Office and the National Physical Laboratory with laboratories at Dollis Hill and Teddington respectively, in cooperation with the Royal Observatory at Greenwich, have done much the same sort of thing in England in relation to time and frequency measurements and broadcast services as has just been described. Considering the number of crystal units among these organizations and the precise nature of the intercomparisons maintained between them, this is probably the most extensive and elaborate quartz clock system in the world. In connection with Greenwich Observatory alone, the complete installation includes eighteen or more such clocks used in deriving the best possible mean rate from steller observations at Greenwich and from studies of other time observatories throughout the world.
An outline description of the quartz clocks of Greenwich Observatory, and of their function there, has been discussed by Humphry M. Smith in Electrical Times116 (London) in March 1946. These clocks employ for the most part the GT cut crystal, first described by W. P. Mason, the bridge stabilized oscillator circuit developed by L. A. Meacham, and the regenerative modulator type of frequency dividers similar to those first developed by R. I. Miller.
The accuracy of the quartz clocks exceeds that of the best pendulum clocks with the result that quartz clocks are now used exclusively in the most precise measurements of time. Some of the considerations117 leading up to the adoption of quartz clocks at Greenwich were discussed in 1937 by H. Spencer Jones, Astronomer Royal. Since then, reports have appeared from time to time by the Astronomer Royal89, 118 and others119 concerning the adoption and use of quartz clocks there.
Some interesting sidelights on this "Precision Timekeeping Revolution" were written by F. Hope-Jones in two articles120 for the Horological Journal during the same year. The quartz clock itself, as developed by the British Post Office for Greenwich Observatory, was described121 in some detail by C. F. Booth in the P.O.E.E. Journal for July 1946. A more general treatment involving some of the same apparatus was presented122 by C.F. Booth and F.J.M. Laver in the I.E.E. Journal of the same month.
An outstanding example of the versatility of the quartz clock has been its application to the measurement of gravity at sea. Knowing of its stable properties and its independence of gravity, Dr. Maurice Ewing in December 1935, asked the Bell Telephone Laboratories whether a portable quartz clock could be made available for use during a proposed gravity measuring expedition by submarine in the West Indies. Since this was in line with experimental work already in progress at the time, the first portable "crystal chronometer", shown in Fig. 33, was assembled for this occasion, and was taken by Ewing and his colleagues in the U.S. Submarine Barracuda on the trip80, 81 which began at Coco Solo on November 30, 1936. This was the first application of the GT crystal and the bridge stabilized oscillator in portable equipment. This original crystal chronometer has been on several gravity-measuring expeditions and is still in active service, having been used again under Dr. Ewing's direction during the summer of 1947.
Fig.
33—Crystal chronometer for geophysical studies, consisting of 100
KC. GT-cut crystal, bridge oscillator, and frequency converters to
derive precision 500-Cycle output to operate timing devices.
Gravity determinations at sea are made by measuring the rate of a special triple pendulum that was invented by F.A. Vening Meinesz especially for use in unsteady environments123. Previously, the standard of rate had been the usual ship's chronometers, but Ewing found the crystal chronometer to be an improvement for his purposes, saying in part: "This chronometer is not thermostatted, and temperatures in a submarine change greatly during a dive. No elaborate control over battery voltages was used. The cruise started in the tropics and ended in Philadelphia in mid-winter. It is highly significant that the interval between NAA-time and the chronometer-time never exceeded 0.6 second during the six-week's cruise and that the variation in this interval is very regular. The crystal chronometer has reduced errors in gravity-measurements at sea, due to the rate of the chronometer, to the point where they are negligible."
Some years previous to the construction of the crystal chronometer, a self-contained quartz clock was made to illustrate the possibility of a compact assembly, but it was not sufficiently portable for the submarine expedition. This earlier clock was regulated by a quartz sphere such as used by 'crystal gazers'. The frequency of the sphere was not adjusted, but its natural frequency, which happened to be 33212, was adopted to operate a mean-time dial by the choice of a suitable gear train. Since that time much more compact assemblies have been built using more suitable crystals for control.
The stable properties of the quartz clock have been useful in a number of cases requiring precise synchronization. Perhaps the most noteworthy among these is the application to Long Range Navigation known as LORAN. In this application, pairs of transmitting stations, usually on shore and separated by accurately known distances, send out distinctive signals in synchronism. The time interval between these signals, as received by a ship, identifies the locus of all the points corresponding to that time interval. The set of curves corresponding to all feasible time intervals defines one of the coordinates in a two-coordinate system. The other coordinate is provided in identical manner by another pair of shore transmitters (which may have one station in common with the first pair). The resulting coordinate system consists of two families of intersecting hyperbolas. From the geometry of these curves, and the constants of the signals, the complete figure bounded by the ship and the transmitters can be determined readily.
The need for stability is evident from the fact that the relation between time error and location error is roughly 5 microseconds per mile. In some cases, location within a mile is highly desirable even at considerable distances. Sometimes the two shore stations, operating as quartz clock time transmitters, must operate for hours without intersynchronization, which calls for very great constancy of rate. One microsecond per hour corresponds to one part in 3.6 X 109.
The precise synchronization of mechanical parts in remotely situated stations can be accomplished readily. For a number of years, the 5-band privacy system of the transatlantic radio telephone service has been thus synchronized, the apparatus at the American terminal being controlled by the Bell System Frequency Standard while that at the English terminal is controlled independently by similar equipment in the British Post Office. The accuracy requirement for this particular purpose is not very great. However, it has been found possible to maintain two or more rotating shafts at remote and independent stations so precisely controlled by independent quartz oscillators that they never depart, during hours of operation, by more than one fifth of one degree of arc.
A major project in which the quartz clock is destined to take an important part is that of making world-wide land and water surveys in order to locate more accurately boundaries and other features of the earth's surface. There would be applications to sea and air navigation and it would be of great value to geophysicists in studying the figure of, and changes in, the earth's surface. By the combination of a widely dispersed set of Photographic Zenith Tubes associated with quartz clocks and time signal means for communication, and with the powerful ranging techniques growing out of LORAN and RADAR, it should be possible to obtain a new order of accuracy in long distance surveying.
The new order of accuracy of time measurement has made it possible for the first time to study directly the variations in longitude caused by the irregular wandering of the poles. These are small effects and heretofore could only be determined by inference from observations of apparent latitude variations at remote stations. With the added new techniques it should be possible to learn a great deal about these and other phenomena related to real or apparent variations in longitude.
Two other possible applications, involving the precise control of angular movement so readily obtainable with synchronous motors operated from quartz crystal controlled alternating current, are of considerable interest. The first is that of operating the right ascension control of a telescope directly from the amplified output of a crystal-controlled low frequency. Vacuum tube amplifiers and synchronous motors are commercially available with which this could be accomplished by suitable gearing. In addition, of course, it would be necessary to include auxiliary controls to allow for atmospheric and other transient effects, and for obtaining rates of motion other than sidereal. For small and slowly changing effects this could be taken care of very simply by means of electrical circuits now well known for adding or subtracting small changes in the control frequency.
The other application refers to a suggestion made by the author a few years ago124 for the measurement of gravity, and changes in gravity, by comparison of the forces Mg and Mw 2R. The proposal was based on the idea that w can be measured or produced with an accuracy two or more orders greater than required, and that the problem reduces to that of balancing two forces and of measuring a linear displacement. The physical set-up would be some form of conical pendulum driven at constant angular velocity about the vertical axis under control of a crystal. Some such arrangements are shown in the reference.
It is part of the nature of a scientist to extrapolate ahead of any current development and to wonder what lies beyond. That feeling is certainly justified in the field of time measurement, for the major advances have taken place in so short a period and so recently, as compared with the thousands of years during which Man has been time-conscious in some degree, that it is reasonable to expect continued advancement for many years to come. Such advancement may come as improvements and refinements in existing techniques, or radically new methods may be developed with inherently more stable potentialities.
Accuracy of Rate
In the first place, it is not reasonable to suppose that the final accuracy that can be attained with the quartz crystal clock has been reached; in view of the rapid current progress indicated in the chart of Fig. 1, it is much too soon to assume this, and there is considerable evidence that improvements could be made by making fuller use of some of the stable properties of quartz crystal and of refinements in the mounting and sustaining circuits. The quartz oscillator assemblies in most general use at the present time embody some compromises which it would not be necessary to make if an all-out effort were being made to construct a few clocks having the highest attainable stability under the most favorable conditions of operation.
The first of these concerns the shape and size of the resonator itself and is related to the frequency of oscillation. From the standpoint of stability of operation, the actual frequency that is used in the oscillator is of little concern because it is now a very simple matter to obtain low frequencies, suitable for the operation of mechanisms, starting with any frequency that can be controlled by a crystal resonator. The choice of 100,000 cycles for the first zero-coefficient resonator was made because, as a standard of frequency, that value was a good median for the range of frequencies then used in electrical communication. For use in a clock any other frequency would answer just as well, so the inherent stability of the resonator should be given first consideration.
One of the inhibitions imposed on the design of quartz resonators has grown out of the dwindling available supply of large pieces of perfect crystal quartz. Where large quantity production is involved this is an important consideration, but for the small numbers required in a few observatories and national laboratories it should not be a limiting factor.
Except for whatever added difficulties might be entailed in the mounting, it seems reasonable that a large resonator should be more stable than a very small one. The most fundamental reason for this is the proportionate change in effective size that would result from the transfer of any surface material including even the quartz itself.
Every substance is supposed to have some vapor pressure although in some cases it is very minute. However, we are concerned with very minute effects, and it is worthwhile to consider what would happen if there were any evaporation or condensation of material. The possibility of this being an important effect is evident when we realize that the removal of a single layer of molecules from the end of a resonator one centimeter long would increase its frequency by about five parts in a hundred million. The effect on frequency would vary about inversely as the effective length, which favors a large crystal. Such a transfer of material could be inhibited to some extent by operating at a low temperature and by seeking equilibrium between the quartz material of the resonator and other quartz material within the same envelope. Of course, other materials than quartz may be involved in similar surface phenomena and should be thoroughly studied and controlled. This has a strong bearing, of course, on the use of conductive materials deposited on a resonator for the purpose of electrical coupling to it.
The slightest trace of surface contamination has a deleterious effect on the damping coefficient. Professor K.S. Van Dyke in 1935 made a series of measurements on resonators of uniform shape and size but constructed with a considerable range of surface treatments45. In the construction of different resonators used in these tests he used different grades of abrasive and various amounts of etching with hydrofluoric acid. In these experiments he operated them under varying degrees of refinement with regard to contamination of the surfaces and found that the highest Q was obtainable only after the utmost care was exercised in keeping the surfaces free from foreign material. The effect is so striking, in fact, that it leads one to wonder whether there is any actual elastic hysteresis in the material of quartz crystal, or whether the minute energy losses observed are entirely surface and coupled effects. Since, for a given shape, the volume increases with linear dimension in greater proportion than the surface area, it can be inferred that surface phenomena would affect a large resonator less than a smaller one.
This is also a reason for employing a stubby shape, in order that the volume of crystal may bear as large a ratio as possible to its surface area. From this standpoint alone a sphere would be ideal but for other reasons, chiefly concerned with the temperature coefficient, it would be unsuitable. It is probable that a polished prolate spheroid, properly oriented with respect to the crystal axes, would satisfy both conditions. Such a resonator could be supported by a pair of wires, serving also as electrical leads from metal-plated electrodes, using techniques already well established.
Crystal resonators as now used in many of the most stable oscillators have been constructed to withstand severe mechanical shock while in operation. It is likely that a slight improvement in frequency stability might be obtained by relaxing a little on the mechanical stability of the present support. Where the greatest accuracy of rate is desired, such as in national standards laboratories and in astronomical observatories, it should be possible to provide suitable mountings for crystal resonators having more delicate supports than those required in mobile equipment. The GT crystal illustrated in Fig. 21 is mounted on eight supporting wires for applications requiring great mechanical stability, and at the same time remains one of the most stable frequency controlling resonators ever produced. It would be reasonable to expect a little improvement in frequency stability at the expense of some mechanical stability if four supports were used instead of eight.
There is a good possibility also that some improvement could be obtained by reducing the electrical coupling to the crystal. At present, the plates are usually provided with plated metal electrodes which cover the entire large surface areas. Some increased stability in frequency might be expected by the use of relatively smaller electrodes covering only the central part of the resonator where the amplitude of vibration is small. At least two advantages might be expected from such a modification. One is that the loading effect is least near the node for vibration, another is that any looseness of material, or elastic hysteresis, would be least troublesome where the motion is least. Of course, it is chiefly the variations in such effects that concern us. One would expect, however, that if such effects exist at all they might be minimized by the use of smaller electrodes.
These particular effects may be eliminated completely, of course, by the use of isolated electrodes spaced from the crystal—but at the expense of other possible variations related to changes in electrode spacing. There is considerable promise in such means, the end result depending upon how precisely the resonator may be held in a fixed position by means that will not change its resonance characteristics. Such means have, in fact, been used successfully in a number of German quartz clocks such as at the Physikalisch-Technische Reichsanstalt108, and with the Dye ring resonator developed by D.W. Dye and L. Essen at the National Physical Laboratory125, 126, England.
For any given resonator and circuit a careful study would probably reveal an optimum amplitude of oscillation that would yield a maximum stability against residual uncontrollable variables. With the GT crystal, as used currently, the maximum amplitude of motion is about 0.00006 mm. It would be possible to limit the motion to a tenth or a hundredth of this value if it should be found desirable.
Further studies of the factors contributing to aging of the quartz material also should produce valuable improvements. Since resonators, which appear to be alike in all other respects, often age at greatly different rates, some being very small or substantially zero, it would seem that some reason should be discoverable for such variations and some effective control established.
There are other relatively massive shapes that should be investigated further such as the ring crystal, mentioned earlier in this paper, and as developed and studied by Dye and Essen125, 126. The ring may be excited in various modes of vibration some of which are more favorable than others from the standpoint of mounting. By choice of orientation relative to the crystal axes, and of dimensions, certain of these can be designed to have zero temperature coefficients in a restricted temperature region.
Another shape that holds great promise because of its convenience of mounting, along with the other desirable properties, is the rectangular rod vibrating longitudinally in its second or higher overtone such as first described by Scheibe and Adelsberger108. Still another possible massive shape is a much thicker version of the GT crystal which would combine the very favorable temperature-frequency characteristic with that of reducing the ratio of surface area to volume.
In seeking the highest possible accuracy a precise temperature control is essential in all cases, even with the GT type of resonator with its wide region of low-temperature coefficient. The reason for this is that the frequency of oscillation depends not only on the mean temperature of the resonator but also upon the temperature gradient throughout its volume. Thus, even if a resonator has the same frequency exactly at different mean temperatures, its frequency will vary a little while the temperature is varying from one value to another. The effect of this can be reduced by enclosing the crystal unit in an envelope with thermal lagging so that such variations as do exist at the temperature control layer are prevented from reaching the crystal. This is no longer a serious problem for there are various electronic means such as described by C.F. Booth and E.J.C. Dixon127 for continuous temperature control, by means of which the variations may be kept very small, and very effective thermal lagging methods128 are well known.
The bridge method for temperature control has been applied in many forms. One of the simplest and most effective procedures has been to utilize a bridge-stabilized oscillator of the type developed by L.A. Meacham for frequency control, and to use it instead for temperature control. For this purpose, all four arms of the bridge are noninductive resistances wound as heaters on the oven to be controlled. In the feedback circuit of the oscillator, a rough frequency control is included simply for the purpose of setting up an oscillation in the circuit which includes the bridge. The conjugate pairs of bridge arms are made of resistance wire with different temperature coefficients and so proportioned that the bridge balances at the desired temperature. The amplitude at which this bridge oscillator oscillates depends upon the temperature departure from the balance value. Since the alternating current output of the oscillator flows in the bridge arms, the amount of heating is proportional to the temperature error, and hence the control is automatic.
An astronomical clock, in addition to having as nearly constant a rate as can be attained, should also be able to operate over long periods of time without change or interruption. The reason for this is that many of the phenomena that are of interest in time measurement occur in continuous succession and the greatest amount of information can be obtained only by the use of clocks with which measurements can be made in unbroken sequence. Quartz clocks that have been used for astronomical purposes to date have not had a very commendable record in this respect and already a good deal has been said in the clock literature about this aspect—as though it were an inherent property of the quartz clock.
However, it is only a matter of simple engineering, making use of techniques and apparatus already well known and available, to design a quartz clock which should operate continuously for many years. A chain is only as strong as its weakest link—and the clock comprises a chain of apparatus parts every link of which must function perfectly and continuously. This chain consists of (1) the crystal-controlled oscillator, (2) a frequency demultiplier to obtain a low frequency to operate a motor, (3) a power amplifier to obtain sufficient current to drive the motor and (4) the motor itself, associated with any of a wide assortment of time signal-producing or measuring equipment. In addition to the links in this chain, a power supply must be maintained, and the temperature of the crystal must be controlled, both continuously.
The crystal itself is no problem as far as continuity of operation is concerned. Its motion is so very small there is no likelihood at all of failure on that account. Mountings are very stable and in all likelihood will be improved. The oscillator circuit, the frequency demultiplier, the power amplifier and the temperature-control circuit are all vacuum-tube devices and deserve special consideration. In all of these circuits, vacuum tubes have been used in some installations which do not have a very long life, some even becoming defective within a year of operation. On the other hand, there are tubes which have been developed for use in continuous telephone circuits where failures would be troublesome and costly. Some of these tubes in current production have an expected life of more than ten years. There is good reason to believe that a quartz clock installation equipped with such vacuum tubes throughout, and engineered so as to make effective use of their special properties, would operate continuously for ten years or more.
The remaining "link" in the chain is the synchronous mechanism operated from the crystal-controlled circuits and used for totalizing continuously the oscillations of the crystal and for producing suitable time signals at specified intervals of time thus measured off in terms of the crystal rate. This mechanism usually consists of a small synchronous (phonic wheel) motor operated from a submultiple of the crystal frequency and geared to commutators or cams or other means for producing the electrical signals used in making time measurements. Many of the troubles in quartz clock installations have occurred in this 'link'. There is every reason to believe, however, that suitable synchronous motors geared to cam-controlled electrical contacts can he built that will operate continuously through many years. To insure long operation it would be desirable to employ motors with low rotation speed in order to reduce bearing wear. With the present knowledge of bearing materials and lubricants, it should be a simple matter to design such a motor that would operate without failure for ten years or more.
A relatively trouble-free electrical time signal producer, suitable for operating under the control of a quartz oscillator, with frequency demultipliers to 100 cycles, could be constructed as indicated schematically in Fig. 34. This is not intended to be an actual design, but is intended to indicate how an apparatus could be designed that would circumvent some of the troubles now experienced which prevent long continuous operation.
Fig. 34. -
Suggestion of elements for a quartz clock for long time continuous
operation.
The basic apparatus consists of a crystal oscillator, presumably 100,000 cycles, with a frequency divider to obtain controlled 100-cycle current to drive the 100-pole phonic wheel motor at one revolution per second. Obviously, other crystal frequencies and step-down ratios could be used, the important thing being to obtain a rotation speed of 1 rps. This is a very low speed for a phonic wheel motor but has the obvious advantage of great simplicity since it permits of controlling seconds devices without the use of gearing. Only one shaft is involved and the bearing problem is reduced to the simplest possible terms. A hardened steel cam, integrally mounted with the phonic wheel rotor, is used to operate a single electrical contact, so connected into the circuits controlled by it that the instant of break is the sole time-determining operation. A break signal is preferable to a make signal chiefly because it is easier to avoid irregular effects, such as result from contact chatter, when a circuit is being opened than when it is being closed. If a pallet of sapphire or ruby is used for the mechanical contact on the cam, and if small currents are used through the contacts, made preferably of platinum-iridium or similar alloy, it would be reasonable to expect trouble-free performance through several hundred million operations.
Ordinarily, the "hunting" of a phonic wheel motor operating on a frequency as low as 100 cycles would cause time errors too large to neglect in a device such as just described. However, by the use of feedback in the motor amplifier circuit, such as indicated schematically in Fig. 34, the effective hunting can be reduced to the point where the time errors caused by it would become negligible for most purposes.
Various circuits could be suggested for
making use of the break signal for timing purposes, the one shown in
Fig. 34 being typical and suitable for various methods of precise
measurement and control. It is capable of providing an electrical
impulse with a steep wave front and of adjustable duration. The grid
of the vacuum tube is normally biased to cutoff by the negative
voltage, 
While the contact is closed, the battery E2,
with resistance R3 in series, is short-circuited. But at
the instant of opening the contact, current flows momentarily in the
circuit including E2, R3, C and R2.
By making E2 positive, and equal to or larger than
E1 numerically, the plate circuit of the tube becomes
conducting for a short interval, the duration of which is determined
by the time-constant of the condenser circuit, each time the contact
is opened. At all other times, the plate circuit is nonconducting.
The sharply defined electrical signal thus produced in the plate
circuit can be used by well-known means for direct time comparison
with signals from other sources.
Making use of the duration of the impulse thus produced, it is possible to use it as a selecting means to isolate a single more precise signal from a continuous chain. For example, the 100-cycle wave controlled by the crystal can be modified by a simple vacuum tube circuit to consist of a continuous sequence of very sharply defined impulses. By using the pulse circuit just described as a bias control on an amplifier, it would be readily possible to select one out of every hundred of these impulses and thus provide an extremely precise seconds signal, the accuracy of which is determined wholly by electronic means.
It would be readily possible to vary the time relation of the seconds signal while in operation, by the use of electrical phase shifters in the driving circuits, or by rotating the stator of the phonic wheel motor, but for long continuous operation it would be desirable to keep the number of apparatus parts comprising the clock at a minimum.
It is not necessary, of course, to employ a complete frequency divider and phonic wheel apparatus for each quartz crystal oscillator. As mentioned previously, the relative time rates of quartz oscillators can be measured with very high precision and be very simple means through a direct comparison of the high frequencies.
Other Means for Precise Rate Control
In addition to making improvements on the quartz crystal resonator, and on methods for sustaining it in vibration, there are two other avenues of investigation which may yield comparable results, with possibly some additional advantages. Not much can be said about them at this time except to point out their possibilities because no appreciable work has been done so far to explore their merits as timekeepers.
The first is in the field of very low temperatures where some quite remarkable properties are obtained. Chief of these for our purpose is the supraconductivity of some metals, and the constancy of shape of most materials, at temperatures in the neighborhood of absolute zero. It seems reasonable to suppose that an electrically-resonant circuit maintained at a temperature in this region could be made to have a very high Q, and very stable dimensions, and so have the chief desirable properties for rate control that obtain in a quartz resonator. Resonant cavities used at high frequencies have many of the properties of other electrical resonant circuits, and in particular their energy dissipation for electric oscillations can be very substantially reduced when cooled to superconducting temperatures. In some experiments made recently at Massachusetts Institute of Technology129 it has been shown that a cavity resonator made of lead, which for 3-cm. waves has a Q of about 2,000 at room temperatures, is so much improved at a temperature of 4 degrees absolute that the Q approaches a million. Such a resonator could be used as the stabilizing element in an oscillator and hence in a clock. The relative stability over long periods could, of course, be determined only by experiment.
Maintenance of the required low temperature would add considerably to the complexity of such a system, but if the advantages were such as to produce a new order of stability, and particularly if it should make possible a clock system with small or zero aging, it certainly should be justified for future time measurement studies.
The other avenue of approach is through
the application of certain resonance phenomena in atoms and
molecules that do not depend upon aggregates of matter as is the
case with all mechanical systems used heretofore in time measuring
means. The extreme fineness of structure and the constancy of atomic
and molecular resonance phenomena have long been recognized through
studies of line spectra, and in the field of spectroscopy these
properties have been used as standards of wavelength ever since the
early studies of Joseph von Fraunhofer, reported in 1815.130 Wavelength, l , and frequency, 
, are associated
by the simple relation 
where 
is equal to the velocity
of light. For visible radiations turns out to be extremely
large, for the red light, 6500Ä, it is 462 million million
vibrations per second. So far, such high frequencies have not been
observable or measurable directly but can only be deduced from
wavelength measurements as just stated—which inevitably involve the
use of man-made standards of length and the combined errors of two
quite different sorts of physical measurements.
It has long been the dream of physicists to find some way to tie in directly with the natural frequencies of atoms and molecules and to derive from them a direct measure of rate, and, of course, of time interval. It has been thought, for example, that the red radiation from cadmium vapor, whose wavelength was measured by C. Fabry and A. Perot in terms of the standard meter as accurately as that standard could be defined, would also make a good standard for time measurements. A step in the right direction was made later by A.A. Michelson whose precise determination of the wavelength of this radiation made possible the redefinition of the International Meter as a definite number of such wavelengths, measured in vacuo. From this definition, it is now possible to duplicate the primary standard of length with great accuracy, and to check such secular changes as may occur in the original standard, the distance between two marks on a metal bar. The constancy of the standard, as defined by Michelson, depends upon properties of primary particles of matter, and upon properties of space, which, as far as human beings are concerned directly appear to be quite independent of time or location. A similar definition of rate, or time interval, is very desirable.
A ray of hope came out of the important work of Nichols and Tear131 who proved that electric waves which could be produced electrically were of the same stuff as radiation from hot bodies. They were able to detect radiation of either sort by the same receiving device and showed that they both had the same properties of refraction, polarization, etc. Later, Cleeton and Williams132 were able to produce continuous electric waves at very high frequencies—corresponding to about 1 cm. wavelength—and to show that they also had the important properties of light waves. Now the range has been extended somewhat more and there are reports138 of experimental generators that can produce continuous waves of a few millimeters wavelength. This is an active development and, of course, the end is not in sight. From continuous waves of any frequency it is believed possible by general techniques now well known to control lower frequencies, and from them eventually all sorts of time measuring and indicating devices as previously described.
Within the last few years, the missing link has been discovered which, with suitable instrumentation, may make it possible to construct a clock controlled by atomic- or molecular-resonance phenomena. There are a great number of resonance phenomena associated with the molecules in a gas, or in molecular beams, which are responsive to electric waves that can be produced continuously by modern vacuum tube means. In some cases, the sharpness of resonance is such that changes of frequency of one part in 108 or less can be detected, leading to the idea that such resonance phenomena may be utilized in some way to control the frequency of a suitable oscillator and hence, through frequency conversion circuits, to control frequencies low enough to operate clocks and other mechanisms. Some of the resonance phenomena in point are in the one-centimeter region, a field that is rapidly being exploited in radar and communication applications. It is to be expected, therefore, that techniques for dealing with such high frequencies will be developed in the near future thus facilitating a study of this new approach to timekeeping. The idea of utilizing such resonance phenomena for the measurement of time was suggested in January, 1945 by Professor I.I. Rabi of Columbia University at an address before the American Physical Society and the American Association of Physics Teachers.
These resonance phenomena, involving the interaction of microwave electromagnetic radiation with atoms or molecules of matter, have been discovered only quite recently and it is likely that a great deal more will be learned about them in the next few years. The results already obtained are very promising and investigations already under way may well lead to the means for creating an entirely new type of standard of time interval and rate—both of prime importance in Physics.
The studies of greatest significance for such purposes now in progress fall in two main branches involving quite different techniques. The actual means for regulating a clock would be quite different in the two methods, but would be possible in either. With what is known up to the present time, however, the construction of such a clock would be a considerable undertaking, especially to make one that would operate over long periods. The two chief phenomena involving atomic or molecular resonances are: (1) the absorption of high-frequency energy in certain materials, particularly in gases, exhibiting ultra-fine absorption spectra; and (2) the deflection of beams of atoms or molecules under special conditions of magnetic and electric fields. The earliest reported work on the absorption of microwaves in gases was done by C. E. Cleeton and N. H. Williams134 in 1934. With the development of improved high-frequency generators and measuring techniques the work has been extended considerably during the last few years by C. H. Townes135, W. E. Good135 and others. It is believed that with modifications of methods, such as used by them, it would be possible to control the frequency of the short-wave generators such as used in making these studies; and, if this can be done, the adaptation for use in time-measuring devices would follow naturally as in the case of any other stable oscillator.
The general method using molecular beams has been a gradual development over some years, but the first published suggestion of the applications which relates closely to this work was made in 1938 when I. I. Rabi, J. R. Zacharias, S. Millman and P. Kusch first used the beam deflection method for measuring nuclear magnetic moments.137 Two articles138, 139 in Reviews of Modern Physics in July 1946 give a good description of the molecular beam method and the results of some studies of fine structure resonance phenomena. The resonance curve shown in Fig. 35 obtained recently by P. Kusch and H. Taub of Columbia University, and hitherto unpublished, illustrates the resolution obtainable by molecular beam methods. According to theory, the actual width of the resonance should be substantially independent of the applied frequency and they expect to be able, when employing frequencies corresponding to centimeter waves, to obtain a hundred or more times this resolution. If this should be realized, it suggests the possibility of a clock with an accuracy of better than one part in 108.
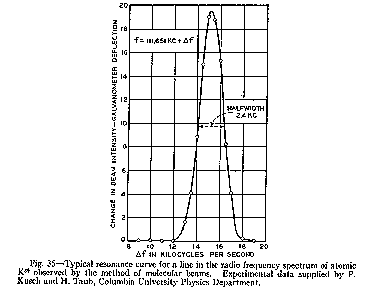
Fig.
35—Typical resonance curve for a line in the radio frequency
spectrum of atomic K39 observed by the method of molecular beams.
Experimental data supplied by P. Kusch and H. Taub, Columbia
University Physics Department.
Perhaps the greatest advantage that might be expected from such a method lies in the possible long-time stability or freedom from aging. Every existing means for timekeeping involves in some manner the motion of large aggregates of matter which, when they rearrange themselves in any way, vary their rates of rotation, or of oscillation, as the case may be, in ways that are not wholly predictable.
It may well develop that a method based on the behavior of single particles of matter will be ageless and, with proper instrumentation, that it will permit of setting up an absolute standard of rate and time interval. The actual value of this rate would be indeterminate by a small amount depending on the sharpness of resonance and the precision of control that could be effected from it, in addition to any uncontrollable effects of the actual resonance frequencies such as result from temperature, pressure, and electromagnetic and gravitational force fields. In the case of some of the resonance phenomena all the latter effects are believed to be vanishingly small. In any case, one would not expect to experience a progressive change in rate as in the case of the rotation of the earth which now is the measure and definition of astronomical time. On the average the earth is said to be slowing down at the rate of a thousandth of a second per day per century140 and, according to the astronomers89, the day will continue to lengthen until finally, at some time in the distant future, the earth will always face one side toward the moon and the length of the day will become about 47 times as long as it is at the present time.
Meanwhile, if an absolute standard could be established, such as now appears feasible through atomic- or molecular-resonance phenomena, it would be possible to record these changes through the centuries and to establish a relatively stable "second" that could be used for all time in physical measurements in place of the elastic second of the cgs system which, as now defined, must stretch with the inevitable variations in the mean solar day.
Whether or not such an "absolute" clock becomes a reality at some time in the future, the quartz crystal clock, because of its accuracy, compactness, great convenience and versatility is likely to continue to be a most useful instrument in all precision measurements of time.
1. The Beginnings of Time-Measurement and the Origins of Our Calendar. James Arthur Foundation Lecture), James Henry Breasted. Published in Book, Time And Its Mysteries, 1936. New York University Press.
2. Encyclopedia Britannica—14th Ed.—"Christian Huygens".
3. Horologium Oscillatorium, Christian Huygens, 1673.
4. Electrical Timekeeping, F. Hope-Jones, N.A.G. Press, London, 1940.
5. Improvements in the Application of Moving Power to Clocks and Timepieces, John Barwise and Alexander Bain, British Patent No. 8783, Filed Jan. 11, 1841, Issued July 10, 1841.
6. The first electric clock, W. A. Marrison, Proceedings of the Engineering Society, Queens University, Kingston, Canada, v. 29, pp. 15-20, 1940.
7. Electric Clocks, F. Hope-Jones Book, N.A.G. Press, London, 1931.
8. Memoire sur l'étude optique des mouvements vibratoires, Jules Lissajous, Comptes Rendus, v. 44, p. 727, April 6, 1857.
9. On the use of the dynamic multiplier with a new accompanying apparatus, C. G. Page, American Journal of Science. 1st Series, 32, 1837, p. 354, dated at Salem Mass. April 24, 1837.
10. Observations on induced electric currents with a description of a magnetic contact breaker, Golding Bird, London, Edinburgh and Dublin, Phil. Mag. Series 3, No. 12, 1838, p. 18. Addressed from Wilmington Square, Nov. 2, 1837.
11. On a new magnetic electric machine, Annals of Electricity, Magnetism and Chemistry and Guardian of Experimental Science, vol. III, pp. 66-70, 1839. Translation from German. Describes apparatus of Dr. Neeff of Frankfurt exhibited at Friburg meeting of Philosophers, September, 1838.
12. Science of Musical Sounds, Dayton Clarence Miller. Book, Macmillan, N.Y. 1916. p. 29.
13. Quelques Experiences d'Acoustique, Rudolph König, Paris, 1882. p. 172.
14. On the characteristics of electrically operated tuning forks, H. M. Dadourian, Physical Review, v. 13, pp. 337-359, May, 1919.
15. Isochronous and Synchronous Movements for Telegraph and Other Lines. Patent No. 203423. Poul la Cour. Filed April 9, 1878.
15a. Roue phonique pour la regularisation du synchronisme des mouvements. Note by P. Ia Cour in Comptes Rendus, v. 87, pp. 499-500, September 25, 1878.
16. Report of Physical Society Meeting of March 30, 1878. Refers to Lord Rayleigh's impulse motor. Nature, May 23, 1878, p. 111.
17. Nouveaux modes d'entretien des diapasons, A. and V. Guillet. Comptes Rendus, v. 130, pp. 1002-1004, April 9, 1900.
18. The Emission of Electricity from Hot Bodies, O.W. Richardson. Book. Longman, Green and Co., London, 1916.
19. On electric discharge between electrodes at different temperature in air and high vacuo, J.A. Fleming, Royal Society of London Proc., v. 47, p. 122, 1890.
20. The Audion—A New Receiver for Wireless Telegraphy, Lee De Forest, A.I.E.E. Transactions, v. 25, pp. 735-779, 1906. Electrician, v. 58, pp. 216-218, 1906.
21. Improvements in instruments for detecting and measuring alternating currents, J.A. Fleming. British Patent No. 24850, 1904.
22. Device for amplifying feeble electrical currents, Lee De Forest. U.S. Patent No. 841387, issued January, 1907.
23. Einrichtung zur Erzeugung elektrischer Schwingungen, Siegmund Strauss. Austrian Patent No. 71340, filed Dec. 1912, issued June, 1915.
24. Improvements in receivers for use in wireless telegraphy and telephony, Marconi Wireless Telegraph Company, Ltd. and Charles Samuel Franklin. British Patent No. 13636, filed June, 1913, accepted June, 1914.
25. Wireless Telegraph and Telephone System, Lee De Forest. U.S. Patent No. 1,507,016, filed September, 1915, issued September, 1924, and U.S. Patent No. 1,507,017, filed March, 1914, issued September, 1924
26. The use of the triode valve in maintaining the vibration of a tuning fork. W.H. Eccles, Phys. Soc. of London Proc., v. 31, p. 269, 1919.
27. Sustaining the vibration of a tuning fork by a triode valve, W.H. Eccles and F. Jordan, The Electrician, v. 82, p. 704, June 20, 1919.
28. Sur L’entretien des oscillations méchaniques au moyen des lampes à trois électrodes, Henri Abraham and Eugene Block, Comptes Rendus, v. 168, pp. 1197-1198, June 16, 1919.
29. Electron tube drive for tuning fork, E.A. Eckhardt, J.C. Karcher, and M. Keiser, Physical Review, v. 17, pp. 535-536, April, 1921.
30. An electron tube tuning fork drive, E.A. Eckhardt, J.C. Karcher and M. Keiser J.O.S.A.-No. 6, pp. 949-957, November, 1922.
31. The valve maintained tooling fork as a precision time standard, D.W. Dye, Royal Soc. of London Proc., v. 103, pp. 240-260, May, 1923.
32. Frequency measurements in electrical communication, J.W. Horton, N.H. Ricker, W.A Marrison. A.I.E.E. Trans., v. 42, pp. 730-741, June, 1923.
33. A celestial encounter, Ernest William Brow, Jl. Franklin Institute, v. 202, pp. 127-163, August 1926.
34. The best observed eclipse in history, Scientific American, March, 1925, p. 155.
35. Precision determination of frequency, J.W. Horton and W.A. Marrison, I.R.E. Proc., v. 16, pp. l37-154, February, 1928.
36. The valve maintained tuning fork as a primary standard of frequency, D.W. Dye and L. Essen, Royal Society of London Proc., v. 143, pp. 285-306, 1934.
37. The anomaly of nickel steels, Charles Edouard Guillaume, Physical Soc. of London Proc., v. 32, p. 374, April, 1928.
38. La compensation des horloges et des montres; precédès nouveaux fondés sur l’emploi des aciers au nickel, Charles Edouard Guillaume. Booklet—Neuchatel et Genève, Paris, 1920.
39. Dilatibilité du chrome et des alliages nickel-chrome dans un intervalle étendu de temperature, Chévenard. Comptes Rendus, v. 174, p 109, January, 1922.
40. Mésure de la dilation du coefficient thermoelastique et propriétès électriques des alliages dans un grand intervalle de temperature. Résultats de l'étude des ferronickels purs et additonnés le chrome. P. Chévenard. Bull. Soc. Franc. Phy. No. 254, pp. 135-138, Dec. 16, 1927.
41. Tuning forks, H. H. Hagland. U.S. Patent 1,715,324, filed June, 1925, issued May, 1929.
42. A mechanical oscillator of constant frequency, August Karolous. U.S. Patent 1,763,853, filed Nov., 1927, issued June, 1930.
43. Compensated Tuning Fork, Bert Eisenhour. U.S. Patent 1,880,923, filed Sept., 1930, issued Oct., 1932.
44. Tuning Fork, S.E. Michaels. U.S. Patent 2,247,960, issued July 1, 1941.
45. A determination of some of the properties of the piezoelectric quartz resonator, Karl S. Van Dyke, Proc. I.R.E., v. 23, No. 4, April, 1935.
46. The high Q of quartz resonators, Maynard Waltz and K.S. Van Dyke, Jl. of Acoustical Soc. of America, v. 19, No. 4, Part 1, p. 732, July, 1947.
47. The crystal clock, W.A. Marrison, National Academy of Sciences Proc., v. 16, pp. 496-507, July, 1930.
48. Development par pression, de l'électricité polaire dans les cristaux hemiedres a faces inclinées, Jacques and Pierre Curie, Comptes Rendus, v. 91, p. 294, 1880.
49. Déformations électrique du quarts, Jacques and Pierre Curie, Comptes Rendus, v. 95, pp. 914-197, 1882.
50. Oeuvres de Pierre Curie, Pierre Curie. Book—Gauthier-Villars, Paris, 1908.
51. The electric network equivalent of a piezoelectric resonator, K.S. Van Dyke, Phys. Rev., v. 25, p. 895, 1925.
52. The piezoelectric effect in the composite rochelle salt crystal, A. McLean Nicolson, A.I.E.E. Trans., v. 38, Part 2, pp. 1467-1485, 1919. A.I.E.E. Proc., v. 38, pp. 1315-1333, 1919.
53. Generating and transmitting electric currents, Alexander M. Nicolson. U.S. Patent No. 2,212,845, filed April 10, 1918, issued August 27, 1940.
54. Sondage par le son, P. Langevin. S. 29, Pub. Spec. No. 3, 1924.
55. Improvements relating to the emission and reception of submarine waves, P. Langevin. French Patent No. 505,903 issued in 1918, also British Patent No. 145,691 issued in 1921.
56. The piezoelectric resonator, W.G. Cady. I.R.E. Proc., v. 10, pp. 83-114, April, 1922.
57. Piezoelektrische Resonanzerscheinungen, A. Scheibe, Zeitschrift für Hochfrequenztechnik, v. 28, No. 1, 1926.
58. Bibliography on piezoelectricity, W.G. Cady, I.R.E. Proc., v. 16, pp. 521-535, 1928.
59. Quarzoszillatoreh, R. Bechmann. Telefunken Zettung, v. 17, pp. 36-45, March 1936.
60. Piezoelectricity, W. G. Cady. Book—McGraw-Hill, New York, 1946.
61. Piezoelectric crystal resonators and crystal oscillators applied to the precision calibration of wave meters, George W. Pierce, Amer. Acad. of Arts and Sciences Proc., v. 59, No. 4, pp. 81-106, October, 1923.
62. Sur un nouvel emploi des quartz piezoélectriques, G. Siadbei, Comptes Rendus, v. 188, p 1390, May, 1929.
63. Piezoelectric crystal oscillators applied to the precision measurement of the velocity of sound in air and carbon dioxide at high frequencies, George W. Pierce, Amer. Acad. of Arts and Sciences Proc., v. 60, pp. 271-302, October, 1925.
64. Sichtbarmachung von hochfrequenten longitudinalschwingungen piezoelektrischen Kristallstabe, E. Giebe and A. Scheibe, Ziets f. physik, v. 33, pp. 335-344, 1925.
65. Leuchtencle piezoelektrische resonatoren als hochfrequenznormale, E. Giebe and A. Scheibe, E.T.Z., v. 47, pp. 380-385, April, 1926.
66. An international comparison of frequency by means of a luminous quartz resonator, S. Jimbo, Proc. I.R.E., v. 18, pp. 1930-1934, 1930.
67. An internationaI comparison of radio wavelength standards by means of pie oelectric resonators W.G. Cady, Proc. l.R.E., v. 12, pp. 805-816, December, 1924.
68. The status of frequency standardization, J.H. Dellinger. Proc. I.R.E., v. 16, No. 5, pp. 579-592, May, 1928.
69. Frequency control system, Warren A. Marrison. U. S. Patent No. 1,788,533, filed March, 1927, issued January, 1931.
70. Precision determination of frequency, J.W. Horton and W.A. Marrison, I.R.E. Proc., v. 16, pp. 137-154, February, 1928.
71. Sur la mésure en valeur absolue des périodes des oscillations electriques de haute fréquence, Henri Abraham et Eugene Block, Comptes Rendus, v. 168, pp. 1105-1108, 1919.
72. "Universal" frequency standardization from a single frequency standard, J.K. Clapp, J.O.S.A ., v. 15, No. 1, pp. 25-47, July, 1927.
73. Frequency demultiplication, Balth Van der Pol and J. Van der Mark, Nature, v. 120, pp. 363-364, Sept., 1927.
74. Uber Relaxationschwingungen, B. Van der Pol, Jr., Zeits. f. Hochfrequenztechnik, v. 29, pp. 114-118, April, 1927.
75. Fractional frequency generators utilizing regenerative modulation, R.L. Miller, I.R.E. Proc., v. 27, No. 7, pp. 446-457, July, 1939.
76. Generation and control of electric waves, Joseph W. Horton, U.S. Patent No. 1,690,299, filed March, 1922, issued November, 1928.
77. Piezoelectric crystal, Warren A. Marrison. U.S. Patent No. 1,899,163, filed Dec., 1928, issued Feb., 1933. U.S. Patent No. 1,907,425, filed Dec., 1928, issued May, 1933. U.S. Patent No. 1,907,426 filed Dec., 1928, issued May, 1933. U.S. Patent No. 1,907,427 filed Dec., 1928, issued May, 1933.
78. A high precision standard of frequency, W.A. Marrison, I.R.E. Proc., v. 17, pp. 1103-1126, July, 1929.
79. The Crystal Clock, W.A. Marrison, National Academy of Sciences Proc., v. 16, pp. 496-507, July, 1930.
80. Gravity measurements on the U.S.S. Barracuda, Maurice Ewing, Transactions of the American Geophysical Union, 1937.
81. Gravity at sea by pendulum observations, Albert J. Hoskinson, American Institute of Mining and Metallurgical Engineers Technical Publication No. 955, New York Meeting, 1938.
82. Modern developments in precision clocks, Alfred L. Loomis and W.A. Marrison, A.I.E.E. Trans., v. 51, pp. 527-537, June, 1932.
83. The precise measurement of time, A.L. Loomis, Monthly Notices, R.A.S., v. 91, March, 1931.
84. The spark chronograph, W. A. Marrison, Bell Laboratories Record, v. 18, No. 2, pp. 54-57, October, 1939.
85. Quartz Crystals for Electrical Circuits, Raymond A. Heising. Book. D. Van Nostrand, Inc. New York, 1946.
86. A new quartz crystal plate, designated the GT, which produces a very constant frequency over a wide temperature range. W.P. Mason. I.R.E. Proc., v. 28, No. 5, pp. 220-223, May, 1940.
87. The bridge stabilized oscillator, L.A. Meacham, I.R.E. Proc., v. 26, No. 10, pp. 1278-1294, October, 1938.
88. Time determination and time broadcast, J. F. Hellweg, Franklin Institute Jl. No. 223, pp. 549-563, 1937.
89. The measurement of time, Sir Harold Spencer Jones, Endeavour, v. 4, pp. 123-130, October, 1945.
90. Translating Circuits (A continuous phase shifter), W. A. Marrison. U.S. Patent No. 1,695,051, filed May, 1925, issued Dec., 1928.
91. Standard Frequency System, W. A. Marrison. U.S. Patent No. 2,087,326, filed Sept., 1934, issued July, 1937.
92. Phase Shifting Apparatus, Larned A. Meacham. U.S. Patent No. 2,004,613, filed Aug., 1933, issued June, 1935.
93. A multiple unit steerable antenna for short wave reception, H.T. Friis and C.B. Feldman, Proc I.R.E., v. 25, pp. 841-915, July, 1937.
94. Clocks showing mean and sidereal time simultaneously, F. Hope-Jones, Franklin Institute Jl. No. 223, pp. 95-100, January, 1937.
95. Sur des horloges indiquant simultanément le temps solaire moyen et le temps sidéral, Ernest Esclangon. Comptes Rendus, 206, pp. 289-292, January 31, 1938.
96. Electrical Engineers' Handbook, Pender-McIlwain. Chapter on Frequency Measurement by W.A. Marrison. John Wiley & Sons, Inc., New York; Chapman & Hall, Ltd., London.
97. Frequency standard, W. A. Marrison. U.S. Patent No. 1,935,325, filed April, 1929, issued Nov., 1933.
98. Frequency measurement, W.A. Marrison. U.S. Patent No. 1,936,683, filed Sept., 1931, issued Nov., 1933.
99. High precision frequency comparisons, L.A. Meacham. The Bridge of Eta Kappa Nu., v. 36, pp. 5-8, Feb.-March, 1940; also Bell System Technical Monograph B-1232.
100. An instrument for short-period frequency comparisons of great accuracy, H.B. Law, The Jl. of the Institution of Electrical Engineers, Vol. 94, Part III, No. 27, pp. 38-41, January, 1947.
101. Electron and Nuclear Counters—Theory and Use, Serge A. Korff. Book. D. Van Nostrand Company, Inc., New York, 1946.
102. Electronic Counters, I.E. Grosdoff, R.C.A. Review, v. 7, No. 3, pp. 438-447, Sept., 1946.
103. Method and Means for Indicating Synchronism, W.A. Marrison. U.S. Patent No. 1,762,725, filed March, 1928, issued June, 1930.
104. Split second time runs today's world, F. Barrows and Catherine Bell Palmer, The National Geographic Magazine, v. 92, No. 3, Sept., 1947. See page 402.
105. Frequency and Time Control Aided by Telephone Company, H. C. Forbes and F. Zaugbaum, Electrical World, pp. 117-118, January 20, 1934.
106. Generation of reference frequencies, L. A. Meacham, Bell Laboratories Record, v. 17, pp. 138-140, January 1939.
107. Eine Quarzuhr für Zeit- und Frequenzmessung sehr hoher Genauigkelt. A. Scheibe und U. Adelsberger. Physikalische Zeitschrift, v. 33, No. 21, pp- 835-841, November, 1932.
108. Die Technischen Einrichtungen der Quarzuhren der Physikalisch-Technischen Reichsanstalt. A. Scheibe und U. Adelsberger. Hochfrequenztechnik und Elektroakustik, v. 43, pp. 37-47, February, 1934.
109. Uber die ersten Erfahrungen mit den Quarzuhren des Preussischen Geodätischen Instituts, E. Kohlschütter. Verhandlungen der Siebenten Tagung der Baltischen Geodätischen Kommission. 1935.
110. German Quartz Clocks. B.l.O.S. Report No. 1316. H.M. Stationery Office, London. See also Science Abstracts B, page 242, September, 1947, and Electrical Engineering Abstracts B, September, 1947.
111. Quartzuhr und Normalfrequencz-Generator, L. Rhode und R. Leonhardt, E.N.T., pp. 117-122, June, 1940.
112. The national primary standard of radio frequency, E. L. Hall, V.E. Heaton and E.G. Clapham. J. Research of National Bureau of Standards, v. 14, pp. 85-98, 1935.
113. Crystal clock for accurate time standard, Vincent E. Heaton, Instruments, v. 20, No. 7, pp. 618-619 July, 1947.
114. W.W.V. standard frequency broadcasts, W.D. George, F.M. and Television, v. 7, pp 25-27, June, 1947.
115. Time service of the U. S. Naval Observatory, J. Frederick Hellweg, Trans. A.I.E.E., v. 51, No. 2, pp. 538-540, June, 1932.
116. Quartz crystal clocks—How Greenwich mean time is determined, Humphry M. Smith, Electrical Times, London, pp. 448-451, March 28, 1946.
117. The Measurement of Time, H. Spencer Jones. Reports on Progress in Physics, v. 4, pp 1-26, 1937. The University Press, Cambridge, 1938.
118. Proceedings of Observatories—Royal Observatory, Greenwich. H. Spencer Jones, Monthly Notices of R.A.S., v. 103, No. 2, pp. 77, 78, 1943.
119. The short-period erratics of free pendulum and quartz clocks, W.M.H. Greaves and L.S.T. Symms, Monthly Notices of R.S.A., v. 103, No. 4, pp. 196-209, 1943.
120. (a) High precision timekeeping—Quartz clock now supersedes free pendulum. F. Hope-Jones, Horological Journal, October, 1943.
120. (b) The precision timekeeping revolution—More about the Quartz Clock. F. Hope-Jones, Horological Journal, November, 1943.
121. A quartz clock, C.F. Booth, P.O.E.E. Journal, v. 39, Part II, pp. 33-37, July, 1946.
122. A standard of frequency and its applications, C. F. Booth and F.J.M. Laver, The Journal of the I.E.E., v. 93, part III, pp. 223-236, July, 1946.
123. Theory and practice of pendulum observations at sea, F.A. Vening Meinesz. Netherlands Geodetic Commission, 1929.
124. Gravitational force measuring apparatus, W.A. Marrison. U.S. Patent No. 2,319,940, filed Sept. 1939, issued May, 1943.
125. The Dye quartz ring as a standard of frequency and time, L. Essen, Proc. Royal Soc., v. 155A, pp. 498-519, July, 1936.
126. A new form of frequency and time standard, L. Essen, Proc. Phys. Soc. of London, v. 50, pp. 413-426, 1938.
127. Crystal oscillators for radio transmitters: An account of experimental work carried out by the Post Office. C.F. Booth and E.J.C. Dixon. Jl. I.E.E., v. 77, pp. 197-236, 1935.
128. Thermostat design for frequency standards, W.A. Marrison, Proc. I.R.E., v. 16, No. 7, pp. 976-980, July, 1928.
129. Superconductivity of lead at 3-cm. wavelength. F. Bitter, J.B. Garrison, J. Halpern, E. Maxwell, J.C. Slater and C.F. Squire, Phys. Rev., v. 70, pp. 97, 98, July 1, 1946.
130. Enc. Brit. 14th Ed. See "Joseph von Fraunhofer".
131. Short Electric Waves, E.F. Nicols and J.D. Tear, Phys. Rev., v. 21, pp. 587-610, June 1923.
132. The shortest continuous waves, C.E. Cleeton and N.H. Williams, Phys Rev., v. 50, p. 1091, December, 1936.
133. A millimeter-wave reflex oscillator, J.M. Lafferty, Jl. of Applied Physics, v. 17, No. 12, pp. 1061-1066, December, 1946.
134. Electromagnetic waves of 1.1 cm. wavelength and the absorption spectrum of ammonia, C.E. Cleeton and N.H. Williams, Phys. Rev., v. 45, pp. 234-237, Feb. 15, 1934.
135. The ammonia spectrum and line shapes near 1.25-cm. wavelength, Charles Hard Townes, Phys. Rev., v. 70, pp. 665-671, November, 1946.
136. The inversion spectrum of ammonia, William E. Good, Phys. Rev., v. 70, pp. 213-218, August, 1946.
137. A new method for measuring nuclear magnetic moments. (Letter to the editor), I.I. Rabi, J.R. Zacharias, S. Millman and P. Kusch, Phys. Rev., v. 53, p. 318, 1938.
138. Molecular beam technique, I. Estermann Reviews of Modern Physics, v. 18, No. 3.
139. The molecular beam magnetic resonance method. The radiofrequency spectra of atoms and molecules. J.B.M. Kellogg and S. Millman, Reviews of Modern Physics, v. 18, No. 3, pp. 323-352, July, 1946.
140. The rotation of the earth, and the secular accelerations of the sun, moon and planets. H. Spencer Jones, Astronomer Royal, Monthly Notices of R.A.S., v. 99, pp. 541-558, May 1939.