


Neil Ashby
University of Colorado
The Global Position System (GPS) consists of 24 earth-orbiting satellites, each carrying accurate, stable atomic clocks. Four satellites are in each of six different orbital planes, of inclination 55 degrees with respect to earth's equator. Orbital periods are 12 hours (sidereal), so that the apparent position of a satellite against the background of stars repeats in 12 hours. Clock-driven transmitters send out synchronous time signals, tagged with the position and time of the transmission event, so that a receiver near the earth can determine its position and time by decoding navigation messages from four satellites to find the transmission event coordinates, and then solving four simultaneous one-way signal propagation equations. Conversely, gamma-ray detectors on the satellites could determine the space-time coordinates of a nuclear event by measuring signal arrival times and solving four one-way propagation delay equations.
Apart possibly from high-energy accelerators, there are no other engineering systems in existence today in which both special and general relativity have so many applications. The system is based on the principle of the constancy of c in a local inertial frame: the Earth-Centered Inertial or ECI frame. Time dilation of moving clocks is significant for clocks in the satellites as well as clocks at rest on earth. The weak principle of equivalence finds expression in the presence of several sources of large gravitational frequency shifts. Also, because the earth and its satellites are in free fall, gravitational frequency shifts arising from the tidal potentials of the moon and sun are only a few parts in 1016 and can be neglected.
The Sagnac effect has an important influence on the system. Since most GPS users are at rest or nearly so on earth's surface, it would be highly desirable to synchronize clocks in a rotating frame fixed to the earth (an Earth-Fixed, Earth-Centered Frame or ECEF Frame). However because the earth rotates, this is prevented by the Sagnac effect, which is large enough in the GPS to be significant. Inconsistencies occurring in synchronization processes conducted on the Earth's surface by using light signals, or with slowly moving portable clocks, are path-dependent and can be many dozens of nanoseconds, too large to tolerate in the GPS. Thus the Sagnac effect forces a different choice for synchronization convention. Also, the path of a signal in the ECEF is not "straight." In the GPS, synchronization is performed in the ECI frame; this solves the problem of path-dependent inconsistencies.
Several sources of relativistic effects enter in determining the unit of time, the SI second as realized by the U. S. Naval Observatory (USNO). For a clock fixed on earth, time dilation arising from earth's spinning motion can be viewed alternatively as a contribution, in the ECEF frame, to the total effective gravitational potential which also includes contributions arising from earth's non-sphericity. Earth-fixed clocks placed on the same equipotential surface of this effective field all beat at the same rate. Over the span of geological time, the earth's figure has distorted so that it nearly matches one of these gravitational equipotentials--the earth's geoid at mean sea level. The SI second is defined by the rate of atomic clocks on the geoid. This rate is determined to sufficient accuracy, relative to clocks at infinity, by three effects: time dilation due to earth's spin, and frequency shifts due to the monopole and quadrupole potentials of earth.
In General Relativity (GR), coordinate time, such as is expressed approximately by a slow-motion, weak-field metric, covers the solar system. The proper time elapsed on a moving clock depends on the clock's position and velocity in the fields of nearby masses, and can be computed in terms of the elapsed coordinate time if the velocities, positions, and masses are known. Conversely, the elapsed coordinate time can be computed by integrating corrections to the proper time.
The concept of coordinate time in a local inertial frame is established for the GPS as follows. In the local ECI frame, imagine a network of atomic clocks at rest and synchronized using constancy of c. To each real, moving clock apply corrections to yield a paper clock which then agrees with one of these hypothetical clocks in the underlying inertial frame, with which the moving clock instantaneously coincides. The time resulting from such corrections is then a coordinate time, free from inconsistencies, whose rate is determined by clocks at rest on the earth's rotating geoid.
Relativistic effects on satellite clocks can be combined in such a way that only two corrections need be considered. First, the average frequency shift of clocks in orbit is corrected downward in frequency by 446.47 parts in 1012. This is a combination of five different sources of relativistic effects: gravitational frequency shifts of ground clocks due to earth's monopole and quadrupole moments, gravitational frequency shifts of the satellite clock, and second-order Doppler shifts from motion of satellite and earth-fixed clocks. Second, if the orbit is eccentric, an additional correction arises from a combination of varying gravitational and motional frequency shifts as the satellite's distance from earth varies. This correction is periodic and is proportional to the orbit eccentricity. For an eccentricity of 0.01, the amplitude of this term is 23 ns. Due to a shortage of computer resources on satellites in the early days of GPS, it was decided that this latter correction was to be the responsibility of software in GPS receivers. It is a correction which must be applied to the broadcast time of signal transmission, to obtain the coordinate time epoch of the transmission event in the ECI frame.
At the time of launch of the first NTS-2 satellite (June 1977), which contained the first Cesium clock to be placed in orbit, there were some who doubted that relativistic effects were real. A frequency synthesizer was built into the satellite clock system so that after launch, if in fact the rate of the clock in its final orbit was that predicted by GR, then the synthesizer could be turned on bringing the clock to the coordinate rate necessary for operation. The atomic clock was first operated for about 20 days to measure its clock rate before turning on the synthesizer. The frequency measured during that interval was +442.5 parts in 1012 faster than clocks on the ground; if left uncorrected this would have resulted in timing errors of about 38,000 nanoseconds per day. The difference between predicted and measured values of the frequency shift was only 3.97 parts in 1012, well within the accuracy capabilities of the orbiting clock. This then gave about a 1% validation of the combined motional and gravitational shifts for a clock at 4.2 earth radii.
At present one cannot easily perform tests of relativity with the system because the SV clocks are actively steered to be within 1 microsecond of Universal Coordinated Time (USNO).
Several relativistic effects are too small to affect the system at current accuracy levels, but may become important as the system is improved; these include gravitational time delays, frequency shifts of clocks in satellites due to earth's quadrupole potential, and space curvature.
This system was intended primarily for navigation by military users having access to encrypted satellite transmissions which are not available to civilian users. Uncertainty of position determination in real time by using the Precise Positioning code is now about 2.4 meters. Averaging over time and over many satellites reduces this uncertainty to the point where some users are currently interested in modeling many effects down to the millimeter level. Even without this impetus, the GPS provides a rich source of examples for the applications of the concepts of relativity.
New and surprising applications of position determination and time transfer based on GPS are continually being invented. Civilian applications include for example, tracking elephants in Africa, studies of crustal plate movements, surveying, mapping, exploration, salvage in the open ocean, vehicle fleet tracking, search and rescue, power line fault location, and synchronization of telecommunications nodes. About 60 manufacturers now produce over 350 different commercial GPS products. Millions of receivers are being made each year; prices of receivers at local hardware stores start in the neighborhood of $200.
The above is a pure-html version of www.phys.lsu.edu/mog/mog9/node9.html.
And below is the juicy part of the original NASA Technical Memorandum 78104, 1977 9th annual PTTI, NTS-2 report (scanned, OCR'd, and manually edited).
James A Buisson, Roger L. Easton, Thomas B. McCaskill
U.S. Naval Research Laboratory (NRL)
// 3 pages skipped //
FREQUENCY DETERMINATION
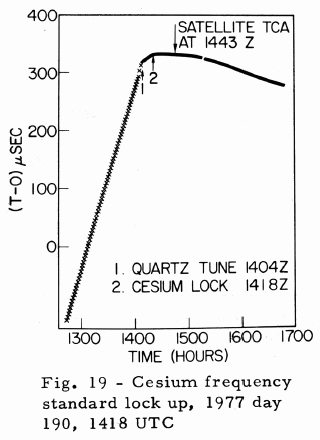
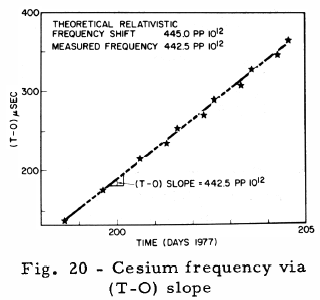
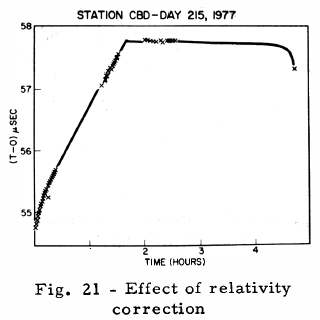
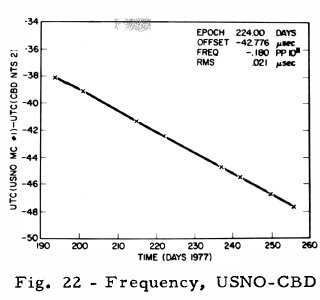
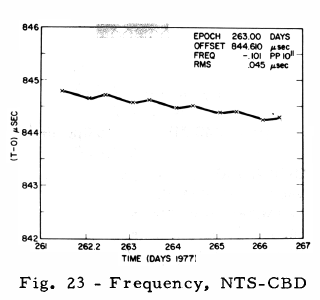
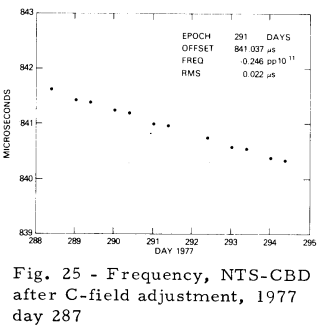
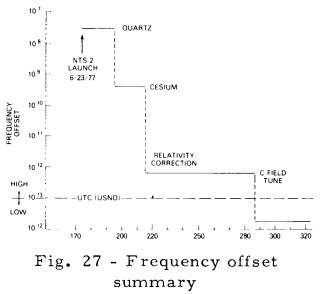
GPS requirements for the NTS-2 mission called for cesium controlled frequency operation after full power was available, following solar panel deployment. The first FTS cesium standard to be used, designated as PRO-5, was locked up (Fig. 19) on the first attempt on Day 190, 1977, at 1418 UTC following a frequency tune to bring the PRO-5 quartz oscillator frequency within the VCXO tuning range of the cesium resonance frequency. Figure 19 presents the theoretical range minus the observed range (T-O) values (13) which are calculated from measurements collected at a one-minute interval from the Panama site. These (T-O) values yield a measure of the spacecraft clock offset with respect to the PMA clock. Knowledge of the station clock offset with respect to the USNO Master clock permits the spacecraft to be referenced to USNO. Figure 20 presents a plot of (T-O) values (13) from PMA over a six day span. The (T-O) slope gives the frequency offset of +442.5 pp1012 with respect to the PMA clock. Inclusion of the PMA frequency offset of +0.6 pp1012 produces an NTS measured value of +443.1 pp1012. Comparison of this value to the predicted value of the relativistic offset of +445.0 pp1012 gives a difference of -3.1 pp1012. On Day 215, 1977, the NTS-2 PRO-5 output signal was offset (Fig. 21) through the use of a frequency synthesizer (4). Closer frequency synchronization to the UTC rate is obtainable by use of cesium C-field tuning which provides a resolution of 1.3 pp1013. Before applying the C-field tune, the NTS-2 frequency offset was re-determined using the CBD station. Figure 22 presents a plot of UTC (USNO MC No. 1) - UTC (CBD), where CBD denotes the clock used for the CBD receiver. The slope of this line yields a frequency offset of 18.0 pp1013. Figure 23 presents a plot of (NTS-CBD); a frequency offset of 10.1 pp1013 was measured. Combining these results Figure 24 produced a frequency offset of +7.9 pp1013. On Day 287, 1977 (14 Oct), a C-field tune of 6 bits was applied. Figure 25 presents a plot of the (T-O)'s after the C-field tune; a resultant frequency of -6.6 pp1013 was measured. The net measured change was 14.5 pp1013 which exceeded the expected value by 6.7 pp1013. Figure 26 presents the preliminary results of the C-field tune; the cause of the small differences are being investigated. A frequency history of NTS-2 since launch is presented by Figure 27, a split logarithmic scale is used so that positive and negative values of frequency offset with respect to UTC (USNO) may be included over a large range.
// 19 pages skipped //
Selected scans form original below. Full NTS-2 article is here.



Figures:


Send comments or questions to: tvb